Функция плотности состояний электронов и дырок
Для определения числа частиц, имеющих энергию в заданном интервале, необходимо, кроме функции распределения 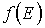 , знать функцию плотности состояний
, знать функцию плотности состояний 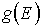 . Эта функция описывает распределение уровней в соответствующих зонах и определяет число уровней, приходящихся на единичный интервал энергии. По определению
. Эта функция описывает распределение уровней в соответствующих зонах и определяет число уровней, приходящихся на единичный интервал энергии. По определению
 (3.8)
(3.8)
Здесь, как и раньше, dZ - число возможных состояний ансамбля частиц (число уровней) с энергией, заключенной в интервале от E до E+dE. Функцию g(E) вычислим для кубического кристалла со стороной L. Энергия электрона у дна зоны проводимости приближенно может быть представлена в виде
 (3.9)
(3.9)
здесь  энергия дна зоны проводимости,
энергия дна зоны проводимости, 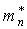 - эффективная масса электрона у дна зоны проводимости, k - квазиимпульс электрона,
- эффективная масса электрона у дна зоны проводимости, k - квазиимпульс электрона,  - его компоненты. Согласно граничным условиям, компоненты квазиимпульса могут принимать только следующие дискретные значения энергии:
- его компоненты. Согласно граничным условиям, компоненты квазиимпульса могут принимать только следующие дискретные значения энергии:



Каждому набору чисел nx, ny, nz отвечает некоторое квантовое состояние (квантовый уровень). В пространстве волновых векторов каждому квантовому состоянию соответствует объем 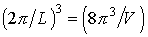 , где V - объем кристалла. Эти элементарные кубические ячейки займут в пространстве волновых чисел объем шара радиусом k, соответствующего максимально возможному значению модуля волнового вектора. Выделим шаровой слой, заключенный между двумя поверхностями k = const и k+dk = const. Объем этого слоя составляет
, где V - объем кристалла. Эти элементарные кубические ячейки займут в пространстве волновых чисел объем шара радиусом k, соответствующего максимально возможному значению модуля волнового вектора. Выделим шаровой слой, заключенный между двумя поверхностями k = const и k+dk = const. Объем этого слоя составляет  . Разделив этот объем на объем элементарной ячейки и умножив на 2, поскольку в каждом состоянии могут находиться по два электрона с противоположно направленными спинами, получим число состояний в объеме шарового слоя:
. Разделив этот объем на объем элементарной ячейки и умножив на 2, поскольку в каждом состоянии могут находиться по два электрона с противоположно направленными спинами, получим число состояний в объеме шарового слоя:
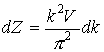 . (3.10)
. (3.10)
Согласно (3.9)

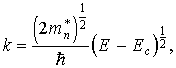

Подставляя значения k2 и dk в формулу (3.10), получим
 .
.
Учитывая (3.8), получим окончательное выражение для плотности квантовых состояний электронов у дна зоны проводимости:
 (3.11)
(3.11)
Энергию дырок у потолка валентной зоны можно записать также в виде параболического закона:
 (3.12)
(3.12)
где Ev - энергия потолка валентной зоны, 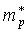 - эффективная масса дырки. Вычисления, аналогичные тем, которые были проведены выше для электронов, приводят к следующему выражению для функции плотности состояний дырок вблизи потолка валентной зоны:
- эффективная масса дырки. Вычисления, аналогичные тем, которые были проведены выше для электронов, приводят к следующему выражению для функции плотности состояний дырок вблизи потолка валентной зоны:
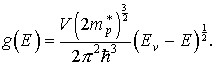 (3.13)
(3.13)
Следует подчеркнуть, что формулы (3.11) и (3.13) справедливы только для состояний вблизи экстремумов энергии, т.е. у дна или потолка энергетической зоны. В средней же части зоны точный вид функции g(E) неизвестен. На рис. 3.4 схематически представлены зависимости плотности квантовых уровней вблизи дна зоны проводимости и потолка валентной зоны.
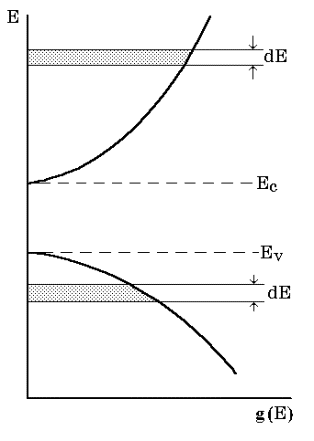 Рис. 3.4. Плотность уровней в зоне проводимости и в валентной зоне
Площадь заштрихованных областей пропорциональна числу уровней в интервале энергий dE
Рис. 3.4. Плотность уровней в зоне проводимости и в валентной зоне
Площадь заштрихованных областей пропорциональна числу уровней в интервале энергий dE
|
Дата добавления: 2021-10-28; просмотров: 412;











