Функция распределения частиц по состояниям. Фермионы и бозоны

Согласно результатам зонной теории твердых тел электроны в кристаллах удобно рассматривать как свободные частицы, эффективная масса которых отличается от массы свободного электрона. В полупроводниках, кроме электронов, носителями заряда являются и положительно заряженные частицы - дырки. Таким образом, в явлениях, в которых основную роль играют эти частицы (электропроводность, теплопроводность, взаимодействие со светом и т.д.) твердое тело можно рассматривать как газ электронов и дырок.

Системы, состоящие из большого количества тождественных частиц, являются предметом изучения статистической физики. Основной особенностью статистических закономерностей является их вероятностный характер. Хорошо известен метод статистического описания коллектива молекул идеального газа. Несмотря на то, что скорость отдельной молекулы газа является величиной случайной в газе, состоящем из большого числа одинаковых молекул, наблюдается определенная закономерность в распределении их по скоростям. Используя методы статистической физики, всегда можно указать, какая доля молекул имеет скорость, заключенную в данном интервале значений.

Основная задача статистики состоит в определении числа частиц, энергия которых лежит в заданном интервале. Результатом решения этой статистической задачи является нахождение функции распределения частиц по энергиям, которую обозначают обычно f(E). Если dZ - число возможных состояний ансамбля частиц с энергией, заключенной в интервале от E до E+dE, а dN - число частиц, находящихся в этих состояниях, то по определению

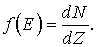(3.1)

Таким образом, функция распределения частиц по энергиям есть плотность заполнения данных состояний частицами.

Для молекул идеального газа f(E) известна как функция распределения Максвелла-Больцмана:

(3.2)

где С - параметр, не зависящий от энергии; k - постоянная Больцмана; Т - абсолютная температура.

Формулу (3.2) называют часто также каноническим распределением или распределением Гиббса. Из этого распределения можно легко получить известное из молекулярной физики распределение Максвелла молекул идеального газа по скоростям теплового движения. Статистика молекул идеального газа исходит из следующих основных положений:

1. Молекулы газа подчиняются законам классической механики.

2. Молекулы газа обладают индивидуальностью, позволяющей отличать их друг от друга. Поэтому, когда две молекулы, находящиеся в разных состояниях меняют местами, это приводит к новому распределению их по состояниям (новому микросостоянию).

3. Предполагается, что все способы распределения равновероятны.

Предположение о том, что электронный газ в металлах подчиняется статистике Максвелла-Больцмана, опровергается рядом экспериментальных результатов. Например, из этого предположения следует, что электроны должны давать вклад в теплоемкость металлов, который примерно на два порядка больше экспериментально наблюдаемой величины. Противоречие снимается, если учитывать квантовые свойства частиц в кристаллах.

В отличие от классической статистики Максвелла-Больцмана квантовая статистика стоит на точке зрения принципиальной неразличимости тождественных частиц. Поэтому перестановка местами двух квантовых частиц не приводит к новому микросостоянию. Для электронов и всех частиц с полуцелым спином необходимо учитывать также принцип Паули. Согласно этому принципу в одном квантовом состоянии может находиться только одна частица. Такие частицы называются фермионами и подчиняются квантовой статистике Ферми-Дирака. Иной квантовой статистикой описываются частицы с нулевым и целым спином. Эти частицы не подчиняются принципу Паули и в одном состоянии их может бытьсколько угодно. Такие частицы называются бозонами, квантовая статистика, которая описывает их распределение по энергиям, - статистикой Бозе-Эйнштейна. Сравнение этих трех статистик приведено на рис. 3.1 на примере распределения двух частиц по трем состояниям. Различные состояния частиц на этом рисунке изображены клетками.

Все возможные способы распределения двух частиц, подчиняющихся классической статистике Максвелла-Больцмана, по трем состояниям показаны на рис. 3.1,а. Поскольку частицы в этой статистике различимы, они обозначены разным цветом. Всего возможно девять микросостояний, математическая вероятность каждого из них равна 1/9. В квантовых статистиках Бозе-Эйнштейна и Ферми-Дирака микросостояния 1 и 2, 3 и 4, 5 и 6 принципиально неразличимы и каждая пара таких состояний должна рассматриваться как одно микросостояние. Для бозонов число возможных микросостояний равно 6 (рис. 3.1,б), а вероятность каждого из них - 1/6. Для фермионов микросостояния, в которых в каждом состоянии находятся по две частицы, реализоваться не могут. Остаются в статистике Ферми-Дирака только три возможных микросостояния, изображенные на рис. 3.1,в. Вероятность каждого из них равна 1/3.

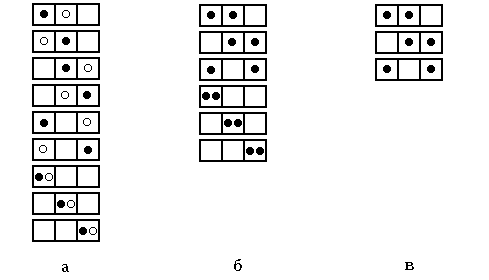Рис. 3.1. Сравнение различных статистик на примере распределения двух частиц по трем состояниям:   а - статистика Максвелла-Больцмана; б - статистика Бозе-Эйнштейна; в - статистика Ферми-Дирака

Статистике Бозе-Эйнштейна подчиняются фотоны и фононы, играющие важную роль в физических свойствах твердых тел. Функция распределения Бозе-Эйнштейна имеет вид

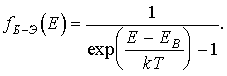(3.3)

Здесь Е_В - химический потенциал системы бозонов.

Если полное число частиц не фиксировано, а должно определяться из условия термодинамического равновесия, как это имеет место для фотонов при излучении абсолютно черного тела, или фононов в кристалле, химический потенциал равен нулю. В этом случае формула (3.3) совпадает с формулой Планка, определяющей среднее число фотонов в данном типе колебаний теплового излучения абсолютно черного тела.