Равновесные и неравновесные носители заряда. Квазиуровни Ферми

Положение уровня Ферми в собственных и примесных полупроводниках связано с концентрацией носителей заряда, установившейсяпри данной температуре в состоянии термодинамического равновесия. Переброс электронов в зону проводимости за счет температурного возбуждения и возникновение в результате этого процесса дырок в валентной зоне называется термической генерацией свободных носителей заряда. Одновременно происходит и обратный процесс: электроны возвращаются в валентную зону, в результате чего исчезают электрон и дырка. Этот процесс называется рекомбинацией носителей заряда. Для количественного описания процессов генерации и рекомбинации носителей заряда в полупроводниках используют понятия скорости генерации, скорости рекомбинации и времени жизни носителей заряда.

Скорость генерации носителей - это число носителей, возбуждаемых в единичном объеме полупроводника за единицу времени.

Скорость рекомбинации носителей - это число носителей, рекомбинирующих в единице объема полупроводника за единицу времени.

Время жизни носителeй  - это среднее время от генерации носителя до его рекомбинации.

Из приведенных выше определений непосредственно следуют следующие соотношения между скоростями рекомбинации электронов R_n и дырок R_p и их временами жизни _n и _p соответственно:

(3.28)

Здесь учтено, что 1/ - вероятность рекомбинации носителя за единицу времени.

При фиксированной температуре устанавливается термодинамическое равновесие, при котором процессы генерации и рекомбинации взаимно уравновешиваются. Такие носители, находящиеся в тепловом равновесии с кристаллической решеткой, называются равновесными.

Электропроводность полупроводника может быть возбуждена и другими способами, например, облучением светом, действием ионизирующих частиц, электрическим полем, инжекцией носителей через контакт и др. Во всех этих случаях дополнительно к равновесным носителям в полупроводнике возникают носители заряда, которые не будут находиться в состоянии теплового равновесия с кристаллом. Такие носители называются неравновесными.

Общую концентрацию электронов в зоне проводимости n в случае равновесных и неравновесных носителей можно представить в виде

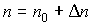, (3.29)

где n₀ – концентрация равновесных электронов; n - концентрация неравновесных электронов.

Общая концентрация дырок

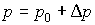, (3.30)

где p₀ и p - равновесная и неравновесная концентрации дырок соответственно.

Поскольку распределение Ферми-Дирака справедливо только для состояния термодинамического равновесия, то понятно, что статистика неравновесных носителей должна быть иной. В отсутствие термодинамического равновесия принято вводить два новых параметра распределения E_Fn для электронов и E_Fp для дырок. Эти параметры выбираюттаким образом, чтобы для концентраций электронов и дырок при наличии неравновесныхносителей выполнялись уравнения (3.17) и (3.19) соответственно при условии замены E_F на E_Fn для электронов и на E_Fp для дырок. Величины E_Fn и E_Fp называют квазиуровнями Ферми электронов и дырок соответственно. Таким образом, в невырожденных полупроводниках справедливы уравнения

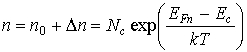, (3.31)

. (3.32)

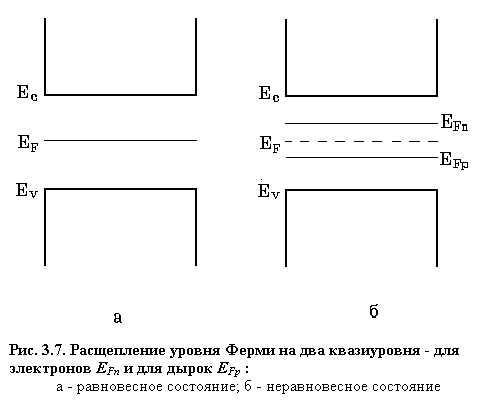
Поскольку при наличии избыточных носителей заряда закон действующих масс не выполняется ( 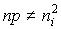), т.к. нет никакой зависимости между n и p, квазиуровни Ферми для электронов и дырок разные и не совпадают с равновесным уровнем Ферми (рис.3.7).

В состоянии термодинамического равновесия квазиуровни Ферми совпадают с равновесным уровнем Ферми E_F. Чем выше концентрация неравновесных носителей заряда, тем дальше отстоят квазиуровниФерми от уровня Ферми. Из уравнений (3.31), (3.32), (3.17) и (3.19) следует

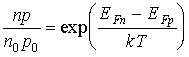. (3.33)

Это соотношение выражает связь между концентрациями электронов и дырок в неравновесном состоянии. Разность энергий 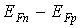характеризует отклонение от состояния термодинамического равновесия. Если np > n₀ · p₀, то . Это условие соответствует инжекции (вбрасыванию) избыточных носителей. Если np < n₀ p₀ , то говорят об экстракции (обеднении) носителей.

Неравновесные носители играют важную роль в работе полупроводниковых приборов.

ГЛАВА 4