Энергия Ферми. Влияние температуры на распределение Ферми-Дирака
Функция распределения Ферми-Дирака, описывающая распределение фермионов по состояниям, имеет следующий вид:
 , (3.4)
, (3.4)
здесь EF - химический потенциал системы фермионов, т.е. работа, которую необходимо затратить, чтобы изменить число частиц в системе на одну. В случае электронов величина EF называется энергией Ферми.
Рассмотрим вид функции Ферми-Дирака при температуре, стремящейся к абсолютному нулю. Как нетрудно видеть из формулы (3.4), для любой энергии частицы, большей энергии Ферми, экспонента в знаменателе стремится к бесконечности при  , следовательно f(Е) стремится к нулю. Это значит, что все энергетические состояния с Е > EF совершенно свободны при абсолютном нуле. Если Е < EF при
, следовательно f(Е) стремится к нулю. Это значит, что все энергетические состояния с Е > EF совершенно свободны при абсолютном нуле. Если Е < EF при  , f(E) стремится к единице. Это значит, что все квантовые состояния с энергией, меньше энергии Ферми, полностью заняты электронами. Отсюда понятен физический смысл энергии Ферми как параметра распределения электронов по состояниям: энергия Ферми есть максимально возможная энергия электронов в металле при температуре абсолютного нуля. Энергетический уровень, соответствующий энергии Ферми, называется уровнем Ферми.
, f(E) стремится к единице. Это значит, что все квантовые состояния с энергией, меньше энергии Ферми, полностью заняты электронами. Отсюда понятен физический смысл энергии Ферми как параметра распределения электронов по состояниям: энергия Ферми есть максимально возможная энергия электронов в металле при температуре абсолютного нуля. Энергетический уровень, соответствующий энергии Ферми, называется уровнем Ферми.
Вид функции распределения Ферми-Дирака при Т = 0К представлен на рис. 3.2,а. На рис. 3.2,б показано распределение электронов по энергетическим уровням в зоне проводимости металла при этой же температуре.
Если Т 0К, то при энергии частицы, равной энергии Ферми, функция распределения Ферми-Дирака равна 1/2. Это значит, что при любой температуре, отличающейся от абсолютного нуля, уровень Ферми заполнен наполовину. Вид функции Ферми-Дирака для двух различных температур показан схематически на рис. 3.3. Изменение характера распределения электронов по состояниям связано с тепловым возбуждением электронов. При этом часть электронов переходит в состояния с энергиями, большей энергии Ферми. Соответственно часть состояний ниже уровня Ферми оказывается свободной. В результате функция f(E) "размыта" вблизи энергии Ферми. Тепловому возбуждению подвергается незначительная часть электронов, находящихся вблизи уровня Ферми. Функция Ферми-Дирака заметно отличается от вида, который она имела при абсолютном нуле, лишь при 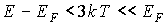 . Величина "размытия" пропорциональна температуре (рис. 3.3). Чем выше температура, тем более существенному изменению подвергается функция распределения.
. Величина "размытия" пропорциональна температуре (рис. 3.3). Чем выше температура, тем более существенному изменению подвергается функция распределения.
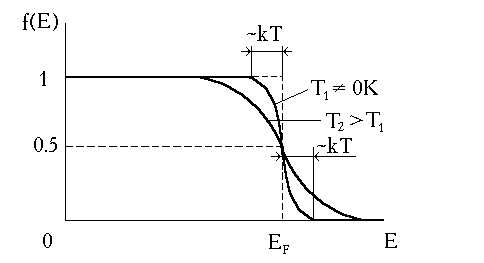 Рис. 3.3. Функция распределения Ферми-Дирака при Т>0K
Рис. 3.3. Функция распределения Ферми-Дирака при Т>0K
|
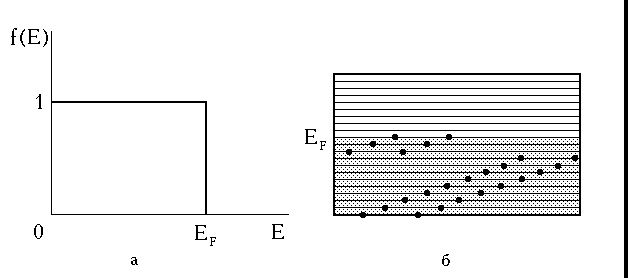 Рис. 3.2. Функция распределения Ферми-Дирака (а) и распределение электронов в зоне проводимости металла при Т=0К (б)
Рис. 3.2. Функция распределения Ферми-Дирака (а) и распределение электронов в зоне проводимости металла при Т=0К (б)
|
При условии
 (3.5)
(3.5)
экспонента в знаменателе становится значительно больше единицы в формуле (3.4). В этом случае единицей можно пренебречь и распределение Ферми-Дирака преобразуется к виду
 (3.6)
(3.6)
Выражение (3.6) совпадает по форме с функцией распределения Максвелла-Больцмана.
Вероятность того, что некоторый энергетический уровень с энергией Е свободен, т.е. занят дыркой, равна
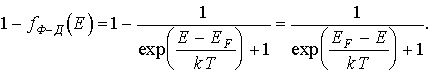 (3.7)
(3.7)
Таким образом, функция распределения Ферми-Дирака для дырок аналогична функции распределения для электронов, если в ней изменить знаки показателей экспонент. Это хорошо согласуется с представлением о том, что дырки являются носителями положительного заряда.
Газ носителей заряда, подчиняющийся статистике Ферми-Дирака, называется вырожденным. Если носители заряда подчиняются статистике Максвелла-Больцмана, то они называются невырожденными.
Дата добавления: 2021-10-28; просмотров: 435;











