ГЕЙЗЕНБЕРГА ДЛЯ СВЕТОВЫХ КВАНТОВ

Цель работы: проверка соотношения неопределенности для квантов света (фотонов) и оценка постоянной Планка h.

Приборы и принадлежности: лазер непрерывного действия видимого диапазона, регулируемая щель, экран, оптическая скамья.

ФИЗИКО-ФИЛОСОФСКОЕ ВВЕДЕНИЕ

Соотношение неопределенности Гейзнберга – фундаментальное положение квантовой теории, утверждающее, что любая физическая система не может находиться в состояниях, в которых координаты ее центра тяжести и импульс принимают одновременно вполне определенные значения. Существуют соотношения неопределенности, связывающие и многие другие физические величины, например энергию и время. Но, в этой работе ограничимся только соотношением неопределенности для динамических переменных – координаты и импульса, поскольку именно они определяют понятие траектории и характер движения микрообъектов.

Чем больше физики узнавали о свойствах света и микрочастиц, тем более осторожными становились их суждения о природе этих объектов. Еще со времен Ньютона и Гюйгенса вплоть до начала нашего века ученые искали ответ на вопрос что такое свет - волна или поток частиц-квантов? После работ де-Бройля (1923 г.) они пытались выяснить: что же такое электрон волна или частица? Лишь с большим трудом постепенно оформилась простая мысль: почему эти свойства - волны и частицы должны исключать друг друга? Ведь логических оснований для альтернативы «или - или» нет. Причина, по которой за нее упорно держались это инерция мышления, из-за которой мы пытаемся осмыслить новые факты с помощью известных понятий и образов, выработанных для описания окружающих нас макроскопических тел.

Сам вопрос «волна или частица?» поставлен некорректно: микрообъект «и волна, и частица» одновременно. Более того, все тела в природе обладают одновременно и волновыми, и корпускулярными свойствами, и свойства эти - лишь различные проявления единого корпускулярно-волнового дуализма. К этой мысли пришли еще в 1924 году Бор, Крамерс и Слэтер. В своей работе они заявили, что «волновой характер распространения света, с одной стороны, и его поглощение и испускание квантами, с другой, являются теми экспериментальными фактами, которые следует положить в основу любой атомной теории и для которых не следует искать каких-либо объяснений».

В формулах Планка Е = hn и де Бройля l = h/mv аналитически отражается непривычное, но несомненное единство свойств «волна - частица».

Частота n и длина волны l - признаки волнового процесса, в то время как, энергия Е и масса m - характеристики частицы. В повседневной жизни мы не замечаем этого дуализма по единственной причине, связанной с малостью постоянной Планка h. Если бы величина постоянной Планка была сравнима с привычными масштабами мира, в котором мы живем, то наши представления о нем резко отличались бы от привычных. Предметы в этом вероятностном мире не имели бы определенных границ, их нельзя было бы произвольно перемещать, и т.д. Но, очень маленькую величину константы Планка 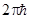= h » 6,626×10-34 Дж×с мы не в состоянии изменить, поэтому этот мир гипотетический. Однако, атомы тоже очень малы и для них этот необычный мир реально существует, и его непривычные законы физикам поневоле приходится принимать так же, как Гулливеру пришлось привыкать к образу мыслей лилипутов.

Пусть, мы захотели описать на математическом языке неделимость свойств «волна - частица». Тогда эти формулы должны установить соотношения между величинами, которые соответствуют понятиям «частица» и «волна». В классической механике эти понятия относятся к различным явлениям природы и строго разделены. В квантовой механике одновременно используются оба понятия и применяются к одному и тому же объекту. Этот подход обусловлен корпускулярно-волновым дуализмом и является вынужденным, за него приходиться дорого платить. Это стало ясно в 1927 году, когда Гейзенберг осознал, что понятия «частица» и «волна» применительно к микрообъектам можно строго определить только порознь.

В физике «определить понятие» означает: «указать способ измерения величины, которая этому понятию соответствует». Гейзенберг постулировал: нельзя одновременно и при этом абсолютно точно измерить координату X и импульс P микрообъекта. Учитывая формулу де Бройля l = h/mv = h/P это означает: нельзя точно и одновременно определить положение Х микрообъекта и длину его волны l. Следовательно, понятия «волна» и «частица» имеют ограниченный смысл, при их одновременном использовании.

Гейзенберг установил количественную меру такого ограничения. Он показал, что если известно положение X и импульс Px микрообъекта с погрешностями Dx и Dpx, то невозможно уточнять эти значения беспредельно, а лишь до тех пор, пока выполняется неравен­ство, названное соотношением неопределенностей: DxDpx ³ h/4p. Хотя этот предел очень мал, но он реально существует, и является фундаментальным. Соотношение неопределенностей это закон природы, никак не связанный с несовершенством наших измерительных приборов. Принципиально невозможно измерить одновременно и координату, и импульс частицы точнее, чем это допускает неравенство DxDpx ³ h/4p. Так же, как нельзя достичь абсолютного нуля температур или сообщить материальному телу скорость, равную скорости света в вакууме.

Удивительно, но многие новые физические теории возникают именно при установлении подобных запретов. Из постулата: «Невозможно построить вечный двигатель»,- родилась термодинамика, из утверждения, что «нельзя превысить скорость света»,- возникла теория относительности. И лишь после того, как физики осознали, что различные свойства квантовых объектов нельзя измерить одновременно с произвольной точностью, квантовая теория сформировалась в окончательном виде.

Соотношение неопределенности можно использовать для оценки по порядку величины некоторых важных физических характеристик микрообъектов. Например, оценим размер атома водорода и энергию электрона в атоме. Хотя понятие траектории движения, определяемой знанием координаты и импульса частицы в каждый момент времени является бессодержательным, за неимением других понятий для оценки энергии электрона в атоме воспользуемся им. Энергия электрона в атоме водорода Е определяется суммой его кинетической энергии

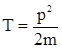
и потенциальной энергии кулоновского взаимодействия

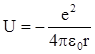, т.е. Е = .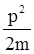

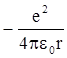В качестве грубой оценки по порядку величины примем за неопределенность координаты г электрона в атоме само значение r, а за меру неопределенности импульса Dр значение р. Тогда соотношение неопределенностей координата - импульс запишется в виде p×r » ħ = h/2p. С учетом этого соотношения выражение для энергии можно переписать следующим образом: E = 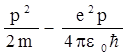. Найдем первую производную энергии Е по импульсу р и приравняем ее нулю: 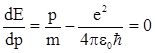. Так как вторая производная по импульсу положительна, то найденное значение р, определяет импульс электрона в атоме с минимальной энергией, т. е. в основном, невозбужденном состоянии, а именно: 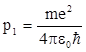. Тогда радиус орбиты электрона в невозбужденном сос­тоянии, так называемый боровский радиус, равен: 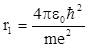, соответственно энергия Е1 невозбужденного состояния равна: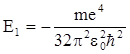

Интересно, что полученные из оценочных формул выражения для Е1 и r1 совпадают с их точными выражениями. Видно, что значение боровского радиуса определяется комбинацией фундаментальных констант, которой можно придать следующий вид:

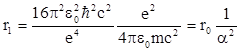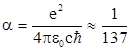, где так называемая постоянная тонкой структуры, 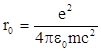- классический радиус электрона, вычисленный в предположении, что собственная энергия уединенного электрона есть энергия его электростатического поля. Тогда скорость электрона на первой боровской орбите
v = ac, т. е. движение электрона в атоме является нерелятивистским. Непосредственная подстановка в полученные формулы значений фундаментальных констант позволяет определить величины r0, r1, E1. Они равны: r0 = 2,8×10-15 м, r1 = 0,5×10-10 м, E1 = -13,6 эВ.

Значение энергии Е обеспечивается кулоновским взаимодействием между электроном и ядром атома водорода - протоном. Из-за малости величины a электрон не может находиться на очень близком расстоянии от ядра и тем более входить в состав ядра. Иначе, неопределенность его координаты определялась бы размерами ядра, но при этом для обеспечения соответствующей неопределенности импульса не хватило бы энергии не только электромагнитного, но ядерного взаимодействия. Соотношение неопределенности позволяет также снять противоречия, возникающие при объяснении так называемого туннельного эффекта, ответственного за процессы ядерного распада, холодной эмиссии электронов из металлов и т.д.