Физические законы электромеханического преобразования энергии
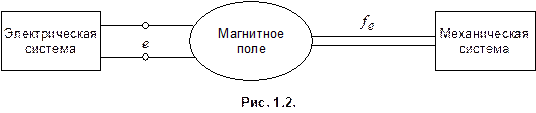
|
Любая электрическая машина представляет собой электромеханический преобразователь энергии. Она объединяет в себе электрическую и механическую системы. Связь между обеими системами в электрической машине осуществляется посредством магнитного поля (рис. 1.2).
Взаимодействие магнитного поля с электрической и механической системами проявляется, с одной стороны, в появлении ЭДС е в элементах электрической системы и, с другой стороны, в возникновении силы 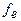 , действующей на элементы механической системы, что и обуславливает электромеханическое преобразование энергии. Процесс такого преобразования подчиняется закону сохранения энергии: изменение энергии, поступающей в электрическую машину со стороны электрической
, действующей на элементы механической системы, что и обуславливает электромеханическое преобразование энергии. Процесс такого преобразования подчиняется закону сохранения энергии: изменение энергии, поступающей в электрическую машину со стороны электрической 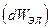 и механической
и механической 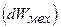 систем, расходуется на изменение энергии магнитного поля
систем, расходуется на изменение энергии магнитного поля 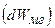 и на покрытие потерь, сопровождающих основной процесс преобразования энергии.
и на покрытие потерь, сопровождающих основной процесс преобразования энергии.
Если все потери в электрической машине вынести во внешние цепи, то уравнение баланса полезного преобразования энергии будет иметь вид
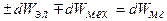 . (1.1)
. (1.1)
Знак «+» означает, что энергия поступает в электрическую машину из внешней системы, а знак «-» - что энергия отдается электрической машиной во внешнюю систему.
Из этого уравнения следует, что процесс преобразования энергии в электрической машине сопровождается непрерывным изменением энергии магнитного поля. Причиной ее изменения является энергия, поступающая либо из электрической, либо из механической системы.
Если в переменное магнитное поле поместить проводящий контур, то в нем возникнет ЭДС
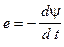 , (1.2)
, (1.2)
где y - потокосцепление контура.
Это явление называется электромагнитной индукцией, а выражение (1.2) представляет собой закон электромагнитной индукции Фарадея. Знак «минус» в формуле для ЭДС е обусловлен инерционным характером магнитного поля: наведенная ЭДС всегда направлена так, что создаваемый ею ток препятствует изменению магнитного поля.
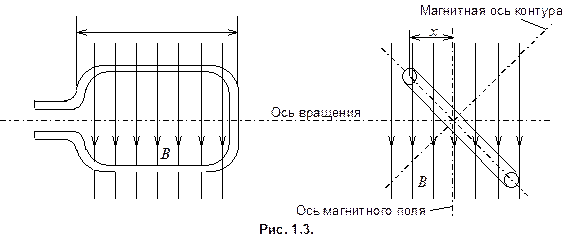
Величина потокосцепления одновиткового контура (рис. 1.3) определяется потоком Ф, пронизывающим площадь S, ограниченную контуром
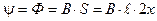 , (1.3)
, (1.3)
где В - магнитная индукция; 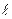 - длина активной части контура; x - смещение плоскости контура относительно оси магнитного поля.
- длина активной части контура; x - смещение плоскости контура относительно оси магнитного поля.
|
Возможны три случая изменения потокосцепления этого контура:
- контур неподвижен, поток меняется во времени;
- контур вращается, поток неизменен;
- контур вращается и поток изменяется во времени.
Поэтому потокосцепление y является функцией пространственной координаты x и времени t ,
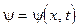 .
.
Следовательно,
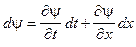 .
.
Подставляя это выражение в (1.2), получим
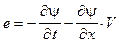 , (1.4)
, (1.4)
где 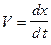 - скорость пересечения контуром силовых линий поля.
- скорость пересечения контуром силовых линий поля.
Согласно (1.4) ЭДС е можно представить в виде двух составляющих: трансформаторной ЭДС 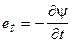 и ЭДС вращения
и ЭДС вращения 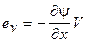 . С учетом выражения для потокосцепления ЭДС вращения может быть записана в виде
. С учетом выражения для потокосцепления ЭДС вращения может быть записана в виде
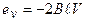 . (1.5)
. (1.5)
Обычно знак «-» в выражении (1.5) опускают, а направление ЭДС определяют правилом правой руки: если правую руку расположить так, чтобы силовые линии входили в ладонь, а отогнутый большой палец направить в сторону перемещения проводника относительно поля, то четыре пальца покажут направление ЭДС. Наличие ЭДС вращения 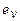 в замкнутом контуре всегда связано с обменом энергией между механической и электрической системами. Существование лишь трансформаторной ЭДС
в замкнутом контуре всегда связано с обменом энергией между механической и электрической системами. Существование лишь трансформаторной ЭДС 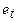 указывает на то, что обмена энергией между механической и электрической системами не происходит.
указывает на то, что обмена энергией между механической и электрической системами не происходит.
Если контур (рис. 1.3) подключить к электрической системе с напряжением u, то по нему потечет ток, величина которого, согласно закону Ома, определяется выражением
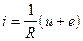 , (1.6)
, (1.6)
где R - активное сопротивление контура.
Ток создает свое магнитное поле (рис. 1.4). Результирующее магнитное поле вокруг проводника искажается: с одной стороны проводника поле усиливается, а с другой - ослабляется. Это приводит к появлению силы, действующей в направлении максимального ослабления поля. Практически направление силы определяется правилом левой руки: силовые линии поля входят в ладонь, четыре пальца показывают направление тока, а отогнутый большой палец показывает направление силы. Поскольку в контуре (рис. 1.5) ток по отношению к внешнему полю протекает в разных направлениях, то на контур будет действовать момент

|
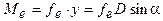 ,
,
где D - диаметр окружности, вписанной в контур; a - угол, определяющий положение контура в магнитном поле.
Если связать контур еще и с механической системой, то можно осуществить передачу энергии в эту систему из электрической системы или наоборот преобразовать механическую энергию в электрическую.
Без учета потерь величина изменения энергии электрической системы определяется выражением
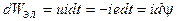 .
.
Соответствующее ей изменение энергии механической системы определяется произведением силы 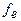 на приращение координаты
на приращение координаты
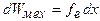 .
.
Закон сохранения энергии (1.1) требует, чтобы суммарное изменение энергии равнялось изменению энергии магнитного поля
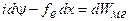 . (1.7)
. (1.7)
Запасенная энергия магнитного поля контура выражается формулой
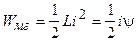 ,
,
где 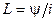 - индуктивность контура.
- индуктивность контура.
Отсюда, учитывая, что ток i задан, получаем
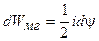 .
.
Подставляя это выражение в уравнение (1.7) и решая его относительно силы 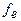 , находим
, находим
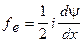 ,
,
или, с учетом (1.3),
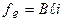 . (1.8)
. (1.8)
Соотношение (1.8) определяет взаимодействие магнитного поля с током электрического контура, помещенного в это поле. Данное взаимодействие проявляется в возникновении силы, действующей на контур. Величина силы пропорциональна магнитной индукции В, току контура i и его активной длине 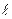 .
.
Дата добавления: 2017-11-21; просмотров: 2516;











