Электроемкость проводников.

Перейдем к рассмотрению весьма важного свойства проводников, называемого их электроемкостью или просто емкостью. Опыт показывает, что разные проводники, будучи заряжены одинаковым количеством электричества, принимают разные потенциалы; это указывает, что они отличаются друг от друга физическим свойством, которое характеризуется величиной, называемой емкостью.

Емкость проводника зависит от расположения окружающих тел, т. к. окружающие тела (даже нейтральные) могут электризоваться (посредством индукции) и менять поле вокруг проводника, а, следовательно, и распределение зарядов на проводнике (что ведет к изменению поля, создаваемого зарядами проводника, и, следовательно, к изменению потенциала, зависящего от данного поля). Потому сперва определим понятие емкости уединенного проводника, т. е. такого проводника, вблизи которого нет никаких других тел, которые могли бы повлиять на распределение на нем зарядов. Потенциал уединенного проводника 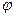пропорционален величине заряда q, так как при увеличении заряда в определенное число раз увеличивается в такое же число раз напряженность поля, а, следовательно, и работа перемещения заряда от проводника в бесконечность:

.

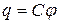Коэффициент пропорциональности С зависит от формы и величины проводника и называется его емкостью. Из последнего равенства имеем:

.

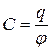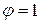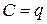Это соотношение указывает, что емкость уединенного проводника есть физическая величина, численно равная количеству электричества, которое надо сообщить ранее не заряженному проводнику, чтобы потенциал его принял значение, равное единице (при имеем ). При этом мы считаем, что неопределенная постоянная в выражении потенциала выбрана так, что потенциалы бесконечно удаленных от проводника точек равны нулю.

В системе СИ за единицу емкости принято брать емкость такого проводника, увеличение на котором заряда на один кулон ведет к повышению его потенциала на один вольт. Такая единица называется фарадом (Ф).

Очевидно, фарад есть чрезвычайно большая единица емкости. В самом деле, это есть емкость уединенного шара радиусом 9 миллионов километров (в 1400 раз большим радиуса земного шара). Практически поэтому наряду с единицей емкости фарадой употребляют меньшую, называемую микрофарадой, равную одной миллионной доле фарады. Емкостью в одну микрофараду обладает уединенный шар радиусом 9 км, т. е. тоже еще очень большой шар.

Конденсаторы.

Уединенные проводники обладают малой емкостью. Даже шар таких размеров, как Земля, имеет емкость всего лишь 700 микрофарад. Вместе с тем на практике бывает потребность в осуществлении системы проводников с большой емкостью, практически не зависящей от окружающих тел. Это оказывается возможным, если система защищена от влияния прочих тел. Примером таких систем являются конденсаторы.

Конденсаторы – это обычно система из двух проводников, называемых обкладками и разделенных диэлектриком, толщина которого мала по сравнению с размерами обкладок. Обкладки конденсатора располагают таким образом, чтобы поле, создаваемое зарядами, находящимися на обкладках, было сосредоточено в пространстве между ними.

Электрическая емкость конденсатора определяется его геометрией и диэлектрическими свойствами среды, заполняющей пространство между обкладками. При зарядке конденсатора на его обкладках появляются заряды, одинаковые по значению, но противоположные по знаку. Разность потенциалов между обкладками изменяется пропорционально заряду.

Простейшими являются плоские конденсаторы – система двух плоскопараллельных проводящих пластин – обкладок, разделенных диэлектриком. Емкость плоского конденсатора вычисляется по формуле

.

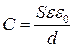Из последней формулы видно, что емкость плоского конденсатора пропорциональна площади пластины S и обратно пропорциональна расстоянию между пластинами d. Чем ближе расположены пластины друг к другу, тем больше емкость образуемого ими конденсатора. Емкость конденсатора также зависит от диэлектрической проницаемости e непроводящей среды, заполняющей пространство между пластинами конденсатора.