Энергия заряженного конденсатора.

Заряженный конденсатор обладает энергией. Для вычисления энергии заряженного конденсатора сначала рассмотрим уединенный незаряженный проводник.

Заряд q, находящийся на некотором проводнике, можно рассматривать как систему точечных зарядов 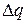. Такая система обладает энергией, равной работе, которую нужно совершить, чтобы перенести все заряды 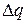из бесконечности и расположить на поверхности проводника.

Перенос из бесконечности на поверхность проводника первой порции заряда 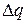не сопровождается совершением работы, так как потенциал проводника первоначально равен нулю. В результате сообщения проводнику заряда 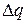его потенциал становится отличным от нуля, вследствие чего перенос второй порции 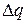уже требует совершения некоторой работы. Так как по мере увеличения заряда на проводнике потенциал его растет, при перемещении каждой последующей порции заряда 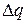должна совершаться все большая по величине работа. Работа, которая совершается против сил поля при сообщении проводнику заряда q и потенциала j является мерой энергии заряженного проводника. Она может быть вычислена по формуле

.

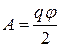Учтя соотношение между емкостью, зарядом и потенциалом проводника, выражение для энергии можно написать

.

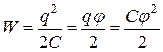Если имеется система двух заряженных проводников (конденсатор), то полная энергия системы равна сумме собственных энергий проводников и энергии их взаимодействия:

,

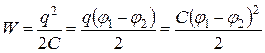где q – заряд одной из обкладок конденсатора, С – емкость конденсатора, j₁ и j₂ – потенциалы соответствующих обкладок, создаваемые как полем другой обкладки, так и собственным полем.