Движение тела, брошенного под углом к горизонту
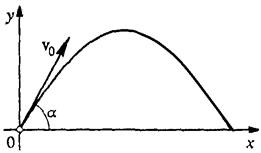
Если телу сообщить начальную скорость 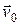 , направленную под углом a к горизонту, то его движение будет криволинейным. Это движение можно рассматривать в плоскости XOY как результат сложения двух прямолинейных движений – равномерного вдоль оси X и равнопеременного по оси Y с ускорением g. Подобные траектории имеют артиллерийские снаряды, футбольные мячи, летящие копья.
, направленную под углом a к горизонту, то его движение будет криволинейным. Это движение можно рассматривать в плоскости XOY как результат сложения двух прямолинейных движений – равномерного вдоль оси X и равнопеременного по оси Y с ускорением g. Подобные траектории имеют артиллерийские снаряды, футбольные мячи, летящие копья.
В выбранной системе отсчета равномерное движение вдоль оси X описывается формулами:
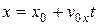 ,
, 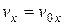 ,
,
где x0 и 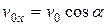 – абсцисса и проекция скорости тела на ось X в момент времени t0.
– абсцисса и проекция скорости тела на ось X в момент времени t0.
Равнопеременное движение вдоль оси Y описывается формулами:
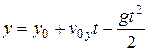 ,
, 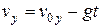 ,
,
где y0 и 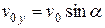 – ордината и проекция скорости тела на ось Y в момент времени t0.
– ордината и проекция скорости тела на ось Y в момент времени t0.
В большинстве задач движение начинается из начала координат (x0=y0=0), поэтому уравнения движения упрощаются:
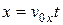 ,
, 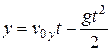 .
.
Найдем траекторию движения тела, избавившись в уравнениях движения от времени t:
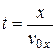 ,
,
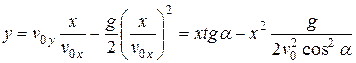 .
.
Т. о., траекторией движения тела является парабола. Дальность полета получим, положив в последней формуле x = L, y = 0:
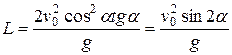 .
.
Наибольшая дальность полета достигается при бросании тела под углом a = 45° к горизонту: здесь sin 2a = sin 90° = 1.
Наибольшую высоту подъема h найдем из условия, что в наивысшей точке проекция скорости на ось Y равна нулю:
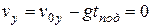 .
.
Откуда найдем время подъема:
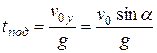 .
.
Тогда
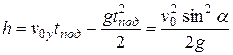 .
.
Наибольшая высота подъема достигается при бросании тела под углом a = 90° к горизонту: здесь sin2a = sin2 90° = 1. В этом случае тело движется прямолинейно вертикально вверх и достигает высоты подъема
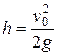 .
.
Дата добавления: 2021-09-25; просмотров: 468;











