Формулы алгебры логики. Функции алгебры логики
Предварительно вспомним некоторые определения из теории множеств. Множество – фундаментальное неопределяемое понятие. Множество – это совокупность объектов, которые, с одной стороны, различны и отличны друг от друга, а с другой стороны воспринимаются как единое целое.
Пусть А и В – два множества и <a,b> – упорядоченная пара, где первый элемент  , а второй элемент
, а второй элемент 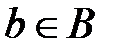 . Декартово произведение
. Декартово произведение 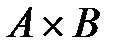 – это множество пар таких что
– это множество пар таких что 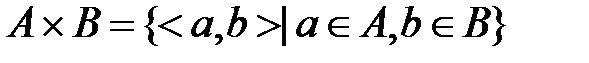 . Бинарным отношением f из множества А в множество В называется подмножество
. Бинарным отношением f из множества А в множество В называется подмножество 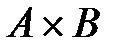 :
: 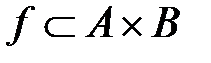 .
.
Функция – это такое отношение, что из 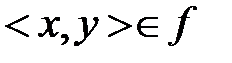 и
и 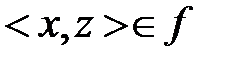 следует, что x=z, то есть функциональность – это однозначность.
следует, что x=z, то есть функциональность – это однозначность.
Пример.
А={1,2,3,4,5}
B={1,4,9,16,25}
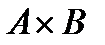 ={<1,1>, <1,4>, <1,9>, <1,16>, <1,25>, <2,1>, <2,4>, <2,9>, <2,16>, <2,25>,….<3,9>, …. ,<4,16>,…..<5,25>}
={<1,1>, <1,4>, <1,9>, <1,16>, <1,25>, <2,1>, <2,4>, <2,9>, <2,16>, <2,25>,….<3,9>, …. ,<4,16>,…..<5,25>}
f={<1,1>, <2,4>, <3,9>, <4,16>, <5,25>} – это функция, где b=a2.
Теперь перейдем к определению булевых функций.
Отличительной особенностью логических функций состоит в том, что они принимают значения в конечных множествах. Иначе говоря, область значений логической функции всегда представляет собой конечную совокупность чисел, символов, понятий, свойств и, вообще, любых объектов.
Если область значений функций содержит k различных элементов, то она называется k-значной функцией.
Определение 1.5.Логическая функция – это функция, в которой переменные принимают только два значения: логическая единица или логический ноль.
Истинность или ложность сложных суждений представляет собой функцию истинности или ложности простых. Эту функцию называют булевой функцией суждений f (a, b).
Логические функции могут зависеть от одной, двух и любого числа переменных (аргументов) х1, …, хn.
В теоретико-множественном смысле логические функции n переменных y=f(x1, …, xn) представляет собой отображение множества наборов (n-мерных векторов, кортежей последовательностей) вида (х1, х2, …, хn) являющегося областью ее определения, на множество ее значений.
Если аргументы принимают значения из того же множества, что и сама функция, то ее называют однородной функцией.
Определение 1.6. Всякая логическая переменная и символы«истина» (1) и «ложь» (0) –формулы.Если Аи В–формулы,то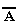 , А
, А  В, А
В, А  В, А
В, А 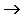 B, А
B, А 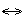 В –формулы.
В –формулы.
Функция 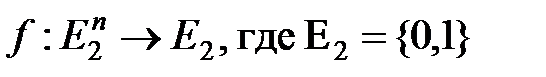 называется функцией алгебры логики.
называется функцией алгебры логики.
y=f(x1,x2) – бинарная функция,
y=f(x1,x2,…., xn) – n- арная функция.
Пример. 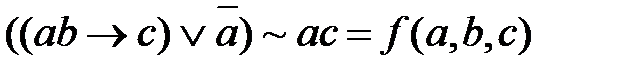
Логическую функцию можно также рассматривать как операцию, заданную законом композиции
Х1  Х2
Х2  …
…  Хn
Хn 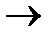 N, где Х1, …, Хn – множества, на которых определены аргументы
N, где Х1, …, Хn – множества, на которых определены аргументы
х1 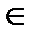 Х1 , х2
Х1 , х2 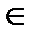 Х2 , …, хn
Х2 , …, хn 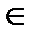 Хn .
Хn .
Если Х1= Х2=…= Хn=N, и однородная функция, рассматриваемая как закон композиции
Nn 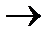 N, определяет n-местную операцию на конечном множестве N.
N, определяет n-местную операцию на конечном множестве N.
Наиболее простым и важнейшим классом однородных функций являются двузначные (булевы) функции (иногда ее называют переключательной). Функция f(x1, x2, …, xn-1, xn) принимает два значения 0,1 и зависит от переменных xi 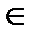 {0,1}, i=
{0,1}, i= 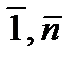 .
.
Областью определения булевой функции служит совокупность всевозможных n-мерных наборов из 0 и 1, а для ее задания достаточно указать, какие значения функции соответствуют каждому из этих наборов, т.е. осуществить табличные значения функции.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой. Совокупность формул образуют функцию.
Таким образом, каждое элементарное высказывание может принимать значение либо 0, либо 1. Каждому набору значений соответствует одно значение всего сложного высказывания (0 или 1).
Любая логическая функция может быть задана с помощью таблицы истинности, в левой части которой записывается набор аргументов, а в правой части – соответствующие значения логической функции.
| x1, x2, …, xn-1, xn | f (x1, x2, …, xn-1, xn) |
| 0 0 … 0 0 | f (0 , 0 , …, 0 , 0) |
| 0 0 … 0 1 | f (0 , 0 , …, 0 , 1) |
| … … … … … | … … …… … … … |
| 1 1 … 1 0 | f (1 , 1 , …, 1 , 0) |
| 1 1 … 1 1 | f (1 , 1 , …, 1 , 1) |
Каждому набору α=(α1, …,αn) αi 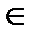 {0,1} становится в соответствии число
{0,1} становится в соответствии число
N=α12n-1+…+ αn-12+ αn.
Наборам (0, 0, …, 0, 0), (0, 0, …, 0, 1), …, (1, 1, …, 1, 1) соответствуют числа 0,1, …, 2n-1.
Легко видеть, что число n-мерных наборов из 0 и 1 равно 2n.
Если зафиксировать n переменных x1, x2, …, xn, то разные функции от переменных x1, x2, …, xn задаются разными таблицами. Число различных таблиц равно числу всех функций от переменных x1, x2, …, xn. Число булевых функций от n переменных x1, x2, …, xn равно 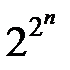 .
.
Переменные, которые принимают значения 0 или 1 называются булевыми переменными. Некоторые функции всегда принимают значение 1 (на любом наборе переменных). Такие функции называются тавтологиями или тождественно истинными. Некоторые функции всегда принимают значение 0 (на любом наборе переменных). Такие функции называются противоречиями или тождественно ложными. Формула называется выполнимой, если существует такой набор значений переменных, при котором эта формула принимает значение 1. Формула называется опровержимой, если существует такой набор значений переменных, при котором эта формула принимает значение 0.
Итак, пусть 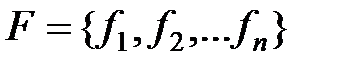 – множество булевых функций. Формулой над F называется выражение
– множество булевых функций. Формулой над F называется выражение 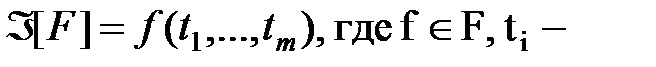 либо переменная, либо формула над F. F называется базисом формулы, f – главной (внешней) операцией, ti – подформулами.
либо переменная, либо формула над F. F называется базисом формулы, f – главной (внешней) операцией, ti – подформулами.
Всякой формуле 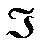 однозначно соответствует некоторая функция f. Это соответствие задается алгоритмом интерпретации, который позволяет вычислить значение функции при заданных значениях переменных.
однозначно соответствует некоторая функция f. Это соответствие задается алгоритмом интерпретации, который позволяет вычислить значение функции при заданных значениях переменных.
Зная таблицы истинности для функций базиса можно вычислить таблицу той функции, которую реализует данная формула.
Примеры.
1. 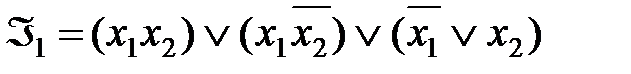
| x1 | x2 | x1 x2 | 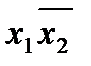
| 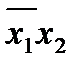
| 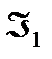
|
Функция 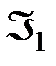 реализует дизъюнкцию на базисе
реализует дизъюнкцию на базисе 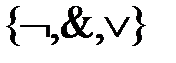 .
.
2. 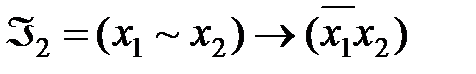
| x1 | x2 | x1~ x2 | 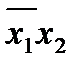
| 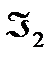
|
Функция 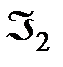 реализует дизъюнкцию на базисе
реализует дизъюнкцию на базисе 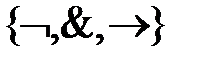 .
.
Таким образом, каждая формула определяет некоторую логическую функцию, которую можно представить в виде таблицы истинности для этой формулы. Если в формуле имеется n переменных, то возможны 2n различных истинностных значений для этой формулы. Следовательно, таблица истинности будет иметь 2n строк.
Функции алгебры логики и их основные свойства.
Рассмотрим множество векторов 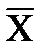 ={x1, x2, …, xn}, пусть координаты этих векторов принимают значения 0 или 1. Таким образом, множество Х состоит из 2n различных векторов.
={x1, x2, …, xn}, пусть координаты этих векторов принимают значения 0 или 1. Таким образом, множество Х состоит из 2n различных векторов.
Совокупность координат некоторого фиксированного вектора 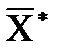 из множества
из множества 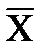 будем называть двоичным набором или просто набором.
будем называть двоичным набором или просто набором.
Сопоставим каждому вектору Х число 0 или 1, т.е. произведем однозначное отображение Х на множество Y={0,1}.
Определение 1.7. Функцией алгебры логики (ФАЛ) называется функция, дающая однозначное отображение Х в Y.
1. Число различных ФАЛ, зависящих от n аргументов, конечно и равно 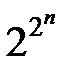 .
.
| x1, x2, …, xn-1, xn | f (x1, x2, …, xn-1, xn) |
| 0 0 … 0 0 | α1 |
| 0 0 … 0 1 | α2 |
| … … … … … | … … …… … … … |
| 1 1 … 1 0 | 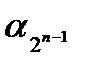
|
| 1 1 … 1 1 | 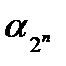
|
Если наборам значений аргументов ФАЛ сопоставляет точки n- мерного пространства, то множество 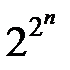 наборов определяет множество вершин n- мерного единичного куба. Таким образом, областью определения ФАЛ, зависящей от n аргументов, является множество вершин такого куба.
наборов определяет множество вершин n- мерного единичного куба. Таким образом, областью определения ФАЛ, зависящей от n аргументов, является множество вершин такого куба.
Пример.
ФАЛ f(x1, x2, x3) может быть задана геометрически. f(101, 110, 010, 011)=1. Значения ФАЛ могут быть заданы не на всех возможных наборах аргументов. На некоторых значения функции могут быть не определены. Такие функции называют не полностью определенными.

2. Если две ФАЛ f1(x1, x2, …, xn-1, xn) и f2(x1, x2, …, xn-1, xn) принимают на всех возможных наборах значений аргументов одинаковые значения, то функции f1 и f2 называются равными.
3. ФАЛ f(x1, x2, …, xi, xi+1, …, xn-1, xn) существенно зависит от аргумента xi, если имеет место соотношение
f(x1, x2, …, xi-1,0 , xi+1, …, xn-1, xn)¹ f(x1, x2, …, xi-1,1 , xi+1, …, xn-1, xn)
в противном случае говорят, что от xi функция зависит не существенно и xi является ее фиктивным аргументом. ФАЛ не изменяется, если к ее аргументам дописать любое число фиктивных аргументов или зачеркнуть те аргументы, которые являются фиктивными.
Как найти несущественные аргументы? Для этого, если ФАЛ задана таблично, поступают следующим образом.
Разбивают множество наборов аргументов функции на два подмножества:
- подмножество, на котором заданная функция принимает значение 1;
- подмножество, на котором заданная функция принимает 0.
Для проверки фиктивности аргумента xi вычеркивают столбец, ему соответствующий, и проверяют, не появились ли в обоих подмножествах одинаковые наборы. Если таких наборов не появилось, то xi является фиктивным аргументом.
Пример:
Таблица
| x1 x2 x3 x4 | f (x1, x2, x3, x4) |
| 0 0 0 0 | |
| 0 0 0 1 | |
| 0 0 1 0 | |
| 0 0 1 1 | |
| 0 1 0 0 | |
| 0 1 0 1 | |
| 0 1 1 0 | |
| 0 1 1 1 | |
| 1 0 0 0 | |
| 1 0 0 1 | |
| 1 0 1 0 | |
| 1 0 1 1 | |
| 1 1 0 0 | |
| 1 1 0 1 | |
| 1 1 1 0 | |
| 1 1 1 1 |
Произведем разбиение набора аргументов:
x1 x2 x3 x4
0 0 0 0
0 0 0 1 x1 x2 x3 x4
0 0 1 0 0 1 0 0
0 0 1 1 наборы х 0 1 0 1
0 1 1 0 на которых 1 1 0 0 f(  )=1
)=1
0 1 1 1 f(  )=0 1 1 0 1
)=0 1 1 0 1
1 0 0 0 1 1 1 0
1 0 0 1 1 1 1 1
1 0 1 1
Вычеркнем в наборах четвертый столбец. Оставшиеся наборы таковы, что ни один из них не входит одновременно в оба подмножества. Это свидетельствует о фиктивности аргумента x4.
Элементарные функции алгебры логики
Рассмотрим множество элементарных ФАЛ. Начнем со случая, когда длина слова n=0. По формуле, определяющей число функций логики, вычисляем, что при n=0 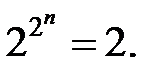
f1=0; f2=1.
Эти две функции совпадают с константами.
В случае n=1 мы имеем две функции, существенно зависящие от аргумента x, эти две функции определяются таблицей
| x1 | f 3 | f 4 |
Эти две функции также относят к элементарным, и они записываются следующим образом
f 3=x ; f 4= 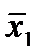 (читается «не x»).
(читается «не x»).
Функцию f 4 называют функцией отрицания.
В случае n=2 имеем десять различных функций, существенно зависящих от аргументов x1 и x2.
| x1Úx2 | x1&x2 | x1~x2 | x1®x2 | x1 ¯ x2 | x1/x2 | x1  x2 x2
| ||
| x 1 | x 2 | f 5 | f 6 | f 7 | f 8 | f 9 | f 10 | f 11 |
Функция f5(x1,x2) =x1Úx2 (дизъюнкция).
Функция f6(x1,x2) =x1&x2 (конъюнкция).
Вместо символов & часто применяют символ умножения «•» или вообще опускают также, как и в обычной алгебре.
Функция f7 носит название функции эквивалентности или функции равнозначности
f7(x1,x2) = x1~x2
и f7(x1,x2) = x1ºx2.
Функция f8 носит название импликации x1 в x2. Она обозначается f8(x1,x2) = x1®x2.
Функция f9 носит название функции Вебба (или ее называют еще стрелкой Пирса) и обозначается
f 9(x1,x2) = x1vx2.
Функция f9 называется функцией (штрихом) Шеффера и обозначается следующим образом f 10(x1,x2) = x1 ¯ x2.
Функция f 11 обычно называется функцией сложения по модулю 2.
f 11(x1,x2) = x1  x2.
x2.
Рассмотрение одиннадцати функций позволяют строить новые функции двумя основными способами:
1. путем перенумерации аргументов;
2. путем подстановки в функцию новых функций вместо аргументов.
Функцию, полученную из функций f 1, f 2, f 3, …, f k путем применения этих правил будем называть суперпозицией функции f 1, f 2, f 3, …, f k .
Имея, например, элементарные функции отрицания, дизъюнкции, эквивалентности и импликации, можно составить следующие новые функции ФАЛ.
Используя таблицы, определяющие элементарные функции, можно задать любую функцию ФАЛ, являющуюся суперпозицией этих функций.
Пример. Пусть требуется представить в виде таблицы следующую функцию
f (x1,x2,x3)={[( 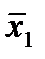 ~x2)Ú (x1 ¯ x2)] (x1
~x2)Ú (x1 ¯ x2)] (x1  x2)}®x3.
x2)}®x3.
Будем строить ФАЛ последовательно.
| x1 | x2 | x3 | 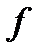 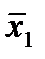
| 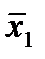 ~x2 ~x2
| x1¯x2 | [ ] | x1  x2 x2
| { } | f (x1,x2,x3) |
Выражение одних элементарных функций через другие
1. Функция f 8(x1,x2) = x1®x2 (импликация x1 в x2) может быть записана посредством функций дизъюнкции и отрицания
x1®x2= 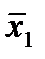 Úx 2.
Úx 2.
Доказательство осуществляется посредством таблиц истинности.
2. Функцию эквивалентности f7(x1,x2)=x1~x2 = x1ºx2 выразим посредством других функций x1~x2= ( 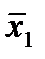 Úx2)&(x 1Ú
Úx2)&(x 1Ú 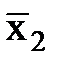 )
)
3. f 11(x1,x2) = x1  x2=
x2=  или f (x1,x2) = x1
или f (x1,x2) = x1  x2=(
x2=( 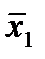 & x2)
& x2)  (x1&
(x1& 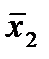 )
)
4. 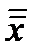 =x
=x
5. x1& x2= 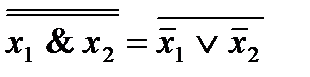
6. x1  x2=
x2= 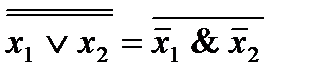
7. x1  x2=
x2= 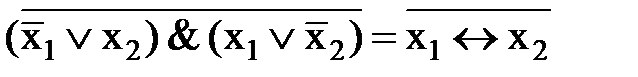
Свойства конъюнкции, дизъюнкции и отрицания
Функции конъюнкции и дизъюнкции обладают рядом свойств, аналогичных свойствам обычных операций умножения и сложения. Легко убедится в том, что для этих функций выполняются законы:
ассоциативности
x1&(x2&x3)= (x1&x2)&x3,
x1  (x2
(x2  x3)= (x1
x3)= (x1  x2)
x2)  x3,
x3,
коммутативности
x1  x2= x1
x2= x1  x2,
x2,
x1& x2= x1&x2,
и дистрибутивности. Кроме того, выполняется закон дистрибутивности дизъюнкции относительно конъюнкции.
x1  (x2&x3)= (x1
(x2&x3)= (x1  x2)& (x1
x2)& (x1  x3).
x3).
Рассмотрим теперь ряд простых, но весьма важных соотношений
х  х=х;
х=х;
х&х=х.
х  1=1; х
1=1; х  0=х; х
0=х; х 
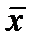 =1;
=1;
х&1=х. х&0=0. х& 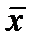 =0.
=0.
И как следствие получаем
х  х
х  …
…  х=х,
х=х,
х&х&…&х=х.
Как обобщение формул получаем следующие формулы, называемые формулами (законами) де Моргана
х1  х2
х2  …
…  хn=
хn=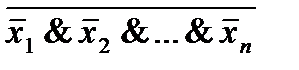 ;
;
х1&х2&…&хn=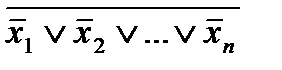 .
.
Свойства функций сложения по модулю 2, импликации, штриха Шеффера и стрелки Пирса (функции Вебба)
Свойства функции сложения по модулю 2 и функции импликации часто бывают полезными при анализе и синтезе различных дискретных устройств.
Для функции сложения по модулю 2 выполняются переместительный и сочетательный законы, а также распределительный закон относительно конъюнкции:
x1 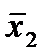 x2= x2
x2= x2  x1;
x1;
x1  (x2
(x2  x3)= (x1
x3)= (x1  x2)
x2)  x3;
x3;
x1&(x2  x3)= (x1&x2)
x3)= (x1&x2)  ( x1&x3).
( x1&x3).
Справедливы также очевидные соотношения
x  x=0;
x=0;
x  0=х;
0=х;
x  1=
1= 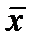 ;
;
х 
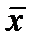 =1.
=1.
Кроме того, выполняется формула х1  х2= x1
х2= x1  x2
x2  x1&x2.
x1&x2.
В отличие от всех ранее рассмотренных функций для импликации не выполняются переместительный и сочетательный законы, однако справедливы следующие соотношения:
х®x=1;
x® 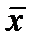 =
= 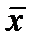 ;
;
x®1=1;
х®0= 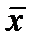 ;
;
0®х=1;
1®х=х;
х1®х2= 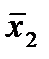 ®
® 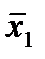 ;
;
х1®х2® х1= х1.
Функции дизъюнкции и конъюнкции могут быть выражены через импликацию следующим образом:
х1  х2=
х2= 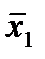 ® х2;
® х2;
х1&х2= 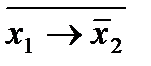 .
.
Для функции Шеффера и Вебба справедлив переместительный закон:
х1 /х2= х2/х1;
х1¯х2= х2¯х1.
Сочетательный закон для них не выполняется:
х1/(х2/х3)¹(х1/х2)/х3 ;
х1¯( х2¯х3)¹ (х1¯ х2)¯ х3.
Справедливы следующие очевидные соотношения, проверка которых аналогична приведенным выше примерам и осуществляется при помощи таблиц истинности:
х /х= 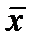 , х¯ х=
, х¯ х= 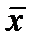 ;
;
х/ 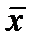 =1, х¯
=1, х¯ 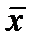 =0;
=0;
х/1= 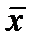 , х¯1 =0;
, х¯1 =0;
х/0=1, х¯0= 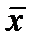 ;
;
х1/х2= 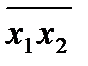 =
= 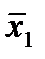

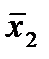 ;
;
х1¯х2= 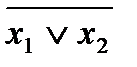 =
= 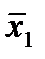 &
& 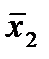 .
.
Функции Шеффера и Вебба связаны между собой соотношениями, аналогичными формулами де Моргана для функций конъюнкции и дизъюнкции:
х1/х2=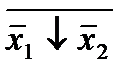 ;
;
х1¯х2=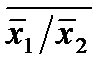 .
.
Дата добавления: 2021-09-25; просмотров: 871;











