Равносильность логических операций.
Одна функция может иметь множество реализаций над данным базисом (т. е. ее можно записать с помощью различных формул). Формулы, реализующие одну и ту же функцию, называют равносильными. Обозначают 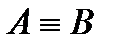 .
.
Пример.
Пусть 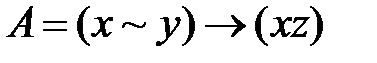 ,
, 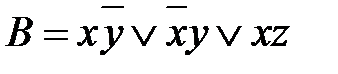 .
.
Доказать, что 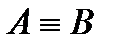 .
.
Равносильность двух формул можно доказать с помощью таблиц истинности. Формулы равносильны, если их значения истинности совпадают на любом наборе значений истинности, входящих в них переменных.
Таблица истинности для формулы А.
| x | y | z | x~y | xz | A |
Таблица истинности для формулы B.
| x | y | z | 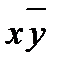
| 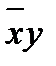
| xz | B |
Тот факт, что равносильность формул логики высказываний можно проверить непосредственно, связан с тем, что переменные, входящие в формулу могут принимать конечное число значений (2n).
Но, если в формуле большое количество переменных, то вычисление всех значений истинности для формулы становится очень трудоемкой задачей.
Равносильность формул логики высказываний аналогична тождествам элементарной алгебры, известным из средней школы. Но тождественное равенство алгебраических формул нельзя проверить простым перебором значений, т. к. число возможных значений переменных неограниченно, следовательно, доказательство равносильности никогда не закончится. В элементарной алгебре тождественные равенства формул устанавливаются с помощью небольшого числа основных тождеств – законов, связывающих между собой арифметические операции.
Для логики имеют место следующие равносильности (рассмотрим только формулы, которые содержат знаки 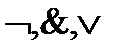 ):
):
1. Коммутативный
АÚВ 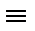 ВÚА АВ=ВА
ВÚА АВ=ВА
2. Ассоциативный
АÚ(ВÚС) 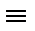 (АÚВ) ÚС А(ВС)=(АВ)С
(АÚВ) ÚС А(ВС)=(АВ)С
3. Дистрибутивный
АÚ(ВС) 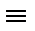 (АÚВ)(АÚС) А(ВÚС)=АВÚАС
(АÚВ)(АÚС) А(ВÚС)=АВÚАС
4. Идемпотентности (Рефлективности)
АÚА 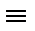 А А·А
А А·А 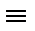 А
А
5. Поглощения
АÚАВ  А А(АÚВ)
А А(АÚВ)  А
А
6. АÚ0  А А· 0 = 0
А А· 0 = 0
7. АÚ1=1 А·1=А
8. АÚ 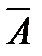 =1 А×
=1 А× 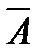 =0
=0
9. Закон де Моргана
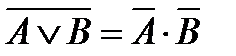
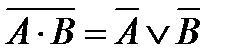
10. 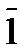 = 0
= 0 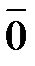 = 1
= 1
11 Двойное отрицание
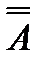 = А
= А
12. А 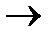 В
В 
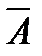 ÚВ
ÚВ
13. А~В=А·ВÚ 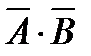
14. А В=
В= 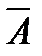 ·ВÚА·
·ВÚА· 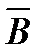
15. А çВ = АÚВ = А·В
16. А ¯ В = 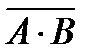 =
= 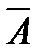 Ú
Ú 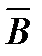
17. Закон склеивания. Закон склеивания базируется на понятии соседних конъюнкций. Соседними называются конъюнкции, отличающиеся представлением одной переменной.
(А^В) Ú ( 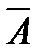 ^B)=B (АÚВ) ^ (
^B)=B (АÚВ) ^ ( 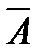 ÚB)=B
ÚB)=B
18. Закон контрапозиции
(А 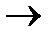 В)
В)  (
( 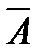
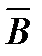 ) (
) ( 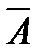
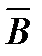 )
)  (А
(А 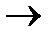 В) (А
В) (А 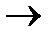
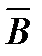 )
)  ( B
( B 
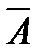 )
)
19. Закон Клавия
( 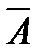
 А)
А)  А
А
20. Закон свертки
АÚ 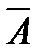 ^B
^B  AÚ B
AÚ B 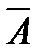 Ú A^ B
Ú A^ B 
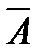 Ú B
Ú B
Примеры. Упростить логическое выражение.
1. 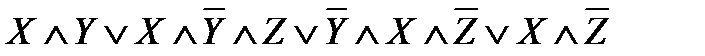
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций:
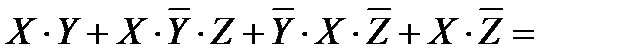
Воспользуемся законом дистрибутивности и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией.
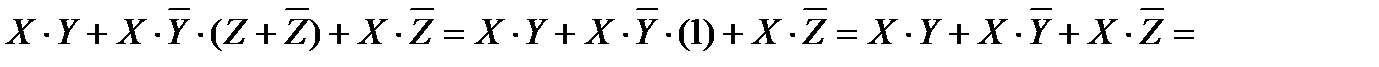
Воспользуемся законом дистрибутивности и вынесем за скобки общий множитель, затем операцией переменной с ее инверсией, затем операцией с константами.
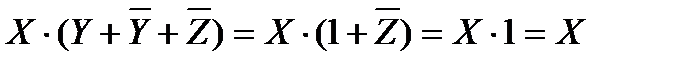
Таким образом, 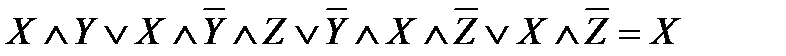
2. 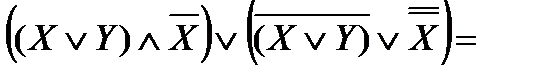
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных дизъюнкцией. Сначала преобразуем выражения в скобках.
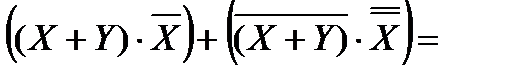
В первой скобке воспользуемся законом дистрибутивности, во второй скобке – раскроем инверсию по правилу де Моргана и избавимся от инверсии по закону двойного отрицания.
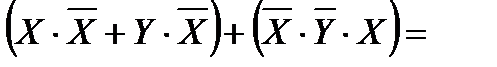
Воспользуемся операцией переменной с ее инверсией.
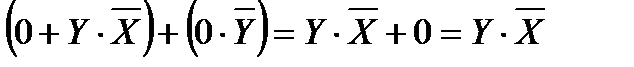
Таким образом, 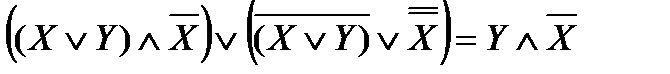
3. 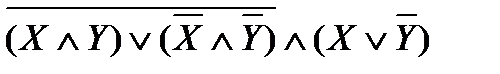
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций. В выражении присутствуют два выражения в скобках, соединенных конъюнкцией. Сначала преобразуем выражения в скобках.
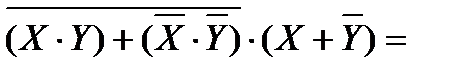
Раскроем инверсию по правилу де Моргана, избавимся от инверсии по закону двойного отрицания.
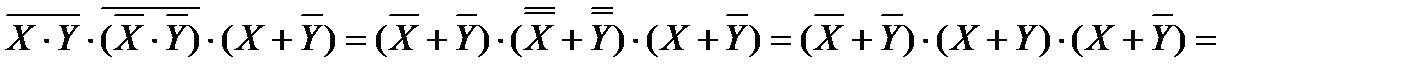
Воспользуемся законом коммутативности и поменяем порядок логических сомножителей.
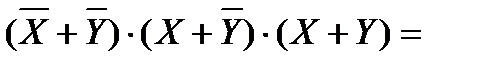
Применим закон склеивания 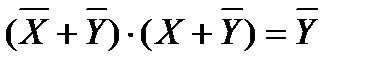
Получим 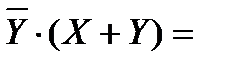
Воспользуемся законом дистрибутивности, затем операцией переменной с ее инверсией, затем операцией с константами.
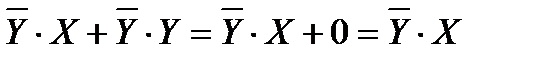
Таким образом, 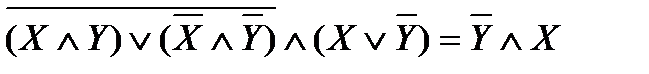
4. 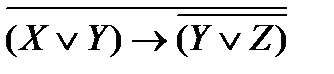
Перепишем выражение с помощью более привычных операций умножения и сложения, определимся с порядком выполнения операций.
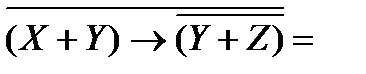
В выражении присутствует импликация. Сначала преобразуем импликацию 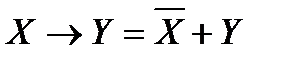 .
.
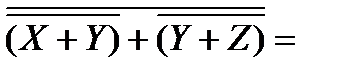
Воспользуемся правилом де Моргана, затем законом двойного отрицания, затем раскроем скобки.
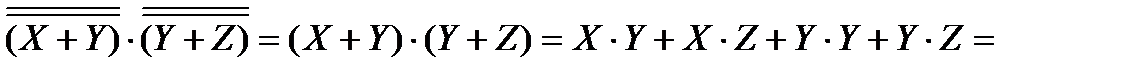
Применим закон идемпотенции и перегруппируем логические слагаемые.
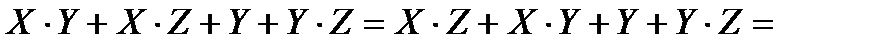
Воспользуемся законом дистрибутивности и вынесем за скобки общий логический множитель. 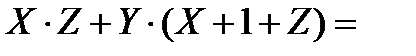
Воспользуемся операцией с константами.
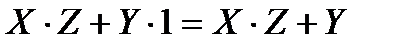
Таким образом, 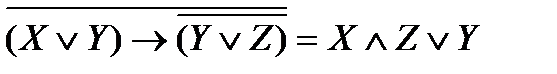
Дата добавления: 2021-09-25; просмотров: 599;











