Логические выражения и логические операции над высказываниями
Определение 1.2. Логическое выражение – это символическая запись, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками).
В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные буквами латинского алфавита A, B, C, …, X, Y ,Z. То есть, чтобы обращаться к логическим высказываниям, им назначают имена. Пусть через А обозначено высказывание «Тимур поедет летом на море», а через В – высказывание «Тимур летом отправится в горы». Тогда составное высказывание «Тимур летом побывает и на море, и в горах» можно кратко записать как А и В. Здесь «и» – логическая связка, А, В – логические переменные, которые могут принимать только два значения – «истина» или «ложь», обозначаемые, соответственно, «1» и «0».
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение. Действия логических операций будем представлять в виде таблиц истинности.
Определение 1.3. Таблица истинности – это табличное представление логической операции (схемы), в котором перечислены все возможные сочетания значений истинности входных переменных (сигналов, операндов) вместе со значением истинности результата операции (выходного сигнала) для каждого из этих сочетаний.
Логические операции:
1. Операция «НЕ»: Операция, выражаемая словом «не», называется инверсией (отрицанием) и обозначается чертой над высказыванием (знаком Ø , либо ¢).
Высказывание 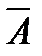 истинно, когда A ложно, и ложно, когда A истинно.
истинно, когда A ложно, и ложно, когда A истинно.
Пример.
А: 7 делится на 5 без остатка.
ØА: Неверно, что 7 делится на 5 без остатка.
| А | ØА |
Эта таблица и принимается в качестве определения операции отрицания.
2. Операция «И»:Операция, выражаемая связкой «и», называется конъюнкцией (лат. conjunctio – соединение) или логическим умножением и обозначается точкой « . » (может также обозначаться знаками  или &).
или &).
Высказывание А × В истинно тогда и только тогда, когда оба высказывания А и В истинны.
Примеры:
A. 6 делится на 3 без остатка (1);
B. 10 больше 5 (1);
C. 7 делится на 3 без остатка (0);
D. 3 больше 7 (0);
A&B=1
A&C=0
C&D=0
| А | В | А&В |
Эта таблица и принимается в качестве определения операции конъюнкции
3. Операция «ИЛИ» Операция, выражаемая связкой «или» (в не исключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio – разделение) или логическим сложением и обозначается знаком  .
.
Высказывание А  В ложно тогда и только тогда, когда оба высказывания А и В ложны.
В ложно тогда и только тогда, когда оба высказывания А и В ложны.
Примеры:
A. 6 делится на 3 без остатка (1);
B. 10 больше 5 (1);
C. 7 делится на 3 без остатка (0);
D. 3 больше 7 (0);
A  B=1
B=1
A  D=1
D=1
C  D=0
D=0
| А | В | А  В В
|
Эта таблица и принимается в качестве определения операции дизъюнкции.
4. Операция «Исключающее ИЛИ» (Операция неравнозначности (равноименности) «строгая дизъюнкция», «сумма по модулю два»,). Строгой дизъюнкцией высказываний А и В называется высказывание, которое истинно тогда и только тогда, когда истинно только одно из этих высказываний. Обозначается знаком  .
.
| А | В | А  В В
|
5. Операция «ЕСЛИ-ТО»: Операция, выражаемая связками «если ..., то», «из ... следует», «... влечет ...», называется импликацией (лат. implico — тесно связаны) или логическим следованиеми обозначается знаком 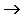 . Высказывание
. Высказывание 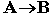 ложно тогда и только тогда, когда А истинно, а В ложно. Высказывание А называется антецедентом, а В – консеквентом.
ложно тогда и только тогда, когда А истинно, а В ложно. Высказывание А называется антецедентом, а В – консеквентом.
| А | В | А 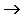 В В
|
6. Операция «РАВНОСИЛЬНО»: Операция, выражаемая связками «тогда и только тогда», «необходимо и достаточно», «... равносильно ...», называется эквиваленцией или двойной импликацией, или логическим тождествоми обозначается знаком 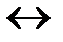 или ~,или
или ~,или  .
.
Высказывание 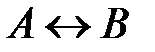 истинно тогда и только тогда, когда значения А и В совпадают.
истинно тогда и только тогда, когда значения А и В совпадают.
| А | В | А~В |
7. Обратная конъюнкция И – НЕ (Штрих Шеффераê)
| А | В | А êВ |
8. Обратная дизъюнкция ИЛИ – НЕ (Стрелка Пирса  , функция Вебба)
, функция Вебба)
| А | В | А  В В
|
Используя эти логические операции можно строить сколь угодно сложные высказывания. Приоритет выполнения операций: ⌐ & Ú 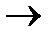 ~
~  ê
ê 
Пример: Сложное высказывание: «Если вы не пропускаете занятия и успешно занимаетесь, то Вы сдадите экзамен хорошо» можно записать следующим образом. Обозначим:
П – пропускаете занятия;
Y – успешно занимаетесь;
Х – сдадите экзамен хорошо,
тогда все высказывание запишется: 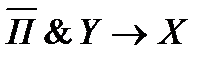
Значение истинности всего выражения будет зависеть от истинности переменных обозначающих простые высказывания.
Пример.
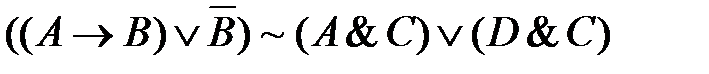
Пусть A=1, B=0, C=0, D=1. Подставим эти значения в высказывание и получим:
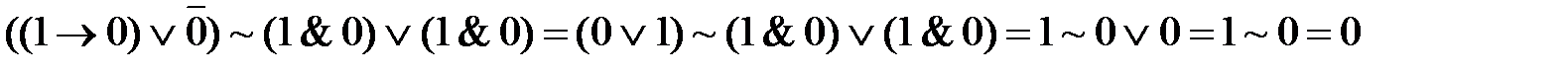
Символы ⌐ & Ú  ~
~  ê
ê  называются пропозициональными связками,
называются пропозициональными связками,
А, В, С, … и т.д. – пропозициональными переменными.
Определение 1.4. Выражение, построенное из пропозициональных переменных с помощью пропозициональных связок, называется пропозициональной формой или формулой.
Пример.
Определить значение истинности составного высказывания
D=А&(А&В 
 )
) 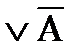 &В
&В
при А=0, В=1, С=1
А&В=0, А&В 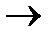 С=1
С=1
А&(А&В 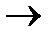 С)=0
С)=0
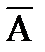 &В=1, D=1.
&В=1, D=1.
Рассмотрим обратную задачу. Пусть D=0. Необходимо найти хотя бы один набор значение высказываний А, В, С, при которых D=0.
В составленном высказывании «D» последней логической операции является дизъюнкция, поэтому составные высказывания должны быть ложны, по определению операции дизъюнкция.
А&(А&В 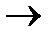 С)=0
С)=0
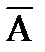 &В=0.
&В=0.
Для того чтобы А&(А&В 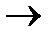
 )=0 , необходимо чтобы или А=0 , или (А&В
)=0 , необходимо чтобы или А=0 , или (А&В 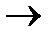
 )=0
)=0
Рассмотрим случай, когда (А&В 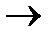
 )=0.
)=0.
Последней операцией здесь является импликация, равная 0 в единственном случае, когда (А&В)=1, а  =0. Отсюда имеем С=1, А=1, В=1. Ясно, что при А=1, В=1 составное высказывание
=0. Отсюда имеем С=1, А=1, В=1. Ясно, что при А=1, В=1 составное высказывание 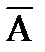 &В=0. Таким образом требуемый набор значений А, В, С определен.
&В=0. Таким образом требуемый набор значений А, В, С определен.
Дата добавления: 2021-09-25; просмотров: 551;











