Частотный критерий устойчивости по ЛАФЧХ. Запасы устойчивости.

Интерпретация критерия для ЛАФЧХ.

Проверка условия (75) может быть выполнена с помощью ЛАФЧХ, наиболее распространенных в инженерной практике. Чтобы посчитать число переходов с помощью ЛАФЧХ рассмотрим, как изменяются эти характеристики при совершении годографом W(jω) перехода.

1.Если АФЧХ W(jω) совершает переход, то фазовая характеристика разомкнутой системы принимает значение 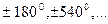. При положительном переходе фаза увеличивается, при отрицательном – уменьшается.

Следовательно для того, чтобы подсчитать число переходов n⁺ и n ^– нужно:

- выделить диапазон частот, где H(ω)>0,

- выделить в этом диапазоне частоты, при которых

φ(ω)= - 180⁰ (1 2k) , k=0,1,2, … ,

- определить, смотря на изменение фазовой характеристики, направление перехода.

Пример ЛАФХ разомкнутой системы приведен на рис.66. Здесь диапазон

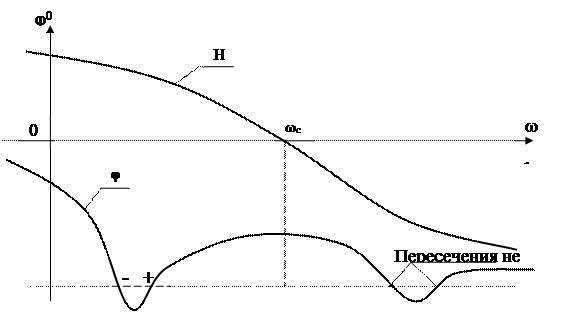Рис.66.

положительности H(ω) находиться левее частоты ω_c (частоты среза). В этом диапазоне из вида ЛФЧХ следует, что имеет место один положительный и один отрицательный переход. При этом, если разомкнутая система устойчива, то замкнутая также устойчива.

Запасы устойчивости САУ.

Критерий Найквиста позволяет ввести широко используемый в инженерной практике понятие запасов устойчивости. Устойчивость – это понятие качественное и нельзя сказать, что система более или менее устойчива. Однако можно ввести характеристики, показывающие, насколько по тому или иному параметру система далека от границы устойчивости. К таким количественным характеристикам относятся запасы устойчивости.

Пусть разомкнутая система устойчива. Рассмотрим годограф W(jω) (см. рис.67.). Выделим на годографе точки, соответствующие пересечению единичной окружности

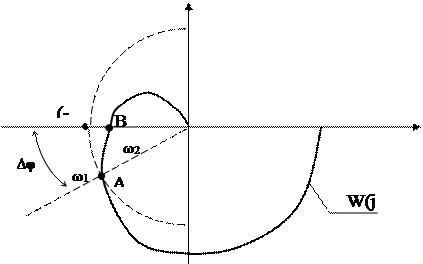Рис.67.

(при частоте w₁) и отрицательной вещественной полуоси (частота ω₂) , т.е.

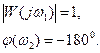
Очевидно что для того, чтобы замкнутая САУ была устойчива нужно, чтобы ω₁>ω₂ . В граничном случае годограф W(jω) проходит через точку (-1,j₀), ω₁=ω₂ и точки А и В совпадают с точкой (-1,j₀). Запасы устойчивости характеризуют удаление точек А и В и всей АФЧХ W(jω) от точки (-1, j₀).

Запас устойчивости по фазе ∆φ характеризует, насколько ФЧХ φ(ω) удалена от -180⁰ в точке, где АЧХ равна единице. Величина ∆φ показывает, насколько может быть ухудшена фаза без изменения АЧХ, чтобы система оказалась на границе устойчивости. Величина ∆φ определяется выражением

∆φ=180⁰+φ(ω₁).

Запас устойчивости по амплитуде ∆А определяется выражением

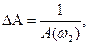
Здесь 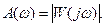Он показывает, во сколько раз может быть увеличена АЧХ без изменения фазовой характеристики, чтобы система оказалась на границе устойчивости.

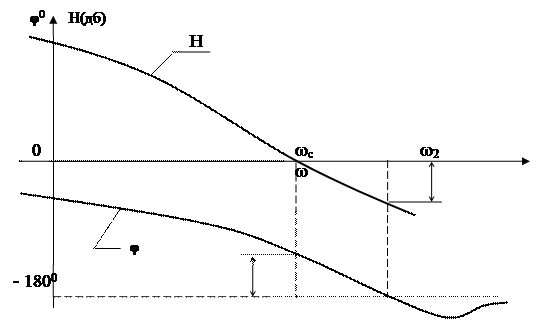
Обычно запасы устойчивости определяют с помощью ЛАФЧХ (см. рис.68).

Рис.68.

При этом частота ω₁ представляет собой частоту среза ω_c , т.е. частоту, на которой H(ω)=0 . Частота ω₂ определяется по пересечению ЛФЧХ –180⁰

При работе с конкретным САУ обычно требуют, чтобы:

- значение запаса устойчивости по фазе составляло

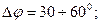
- значение запаса устойчивости по амплитуде составляло в логарифмическом масштабе

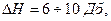
чему для обычной АФЧХ A(ω) соответствует