Пространство Д-параметров.

Критерии устойчивости позволяют выяснить, устойчива или нет автоматическая система. При этом предполагают, что все параметры системы заданы. Однако, часто задача ставится так: заданы все параметры, кроме одного или двух. Необходимо установить, при каких значениях этих параметров САУ будет устойчивой, т.е. ставится задача выделения областей устойчивости по одному или двум параметрам.

Общая теория построения областей с одинаковым числом левых корней характеристического уравнения была разработана Ю.И. Неймарком в 1948г. Рассмотрим характеристические уравнения САУ

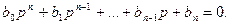
Приведем его к виду

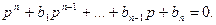(77)

здесь b₀ =1 , получающаяся делением обеих частей уравнения на b₀ .

Примем значения коэффициентов 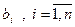за переменные и введем пространство Д параметров – коэффициентов характеристического уравнения (77). Некоторой точке этого пространства соответствуют определенные коэффициенты 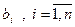и, следовательно, вполне определенные значения корней характеристического уравнения. Разобьем пространство Д поверхностью на ряд областей так, чтобы точкам одной области соответствовало определенное число левых корней характеристического уравнения (77).

Если уравнение (77) имеет степень n, то очевидно, что таких областей в пространстве Д будет n+1. Это области Д₀, Д₁, Д₂, …Д_n , точкам соответствуют коэффициенты 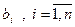такие, что характеристическое уравнение (77) имеет соответственно 0,1,2,…,n корней в левой полуплоскости плоскости “p”. Очевидно, что областью устойчивости будет область Д_n, так как именно в этом случае все корни характеристического уравнения (77) удовлетворяют условию

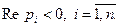
Предположим, что разбивка пространства Д поверхностью на области Д₀, Д₁, Д₂, …Д_n произведена. Предположим также, что некоторым заданным значениям коэффициентов соответствует точка T(b₁,b₂,…,b_n), принадлежащая области Д_к. Следовательно, заданным значениям коэффициентов соответствует к левых и n-k правых корней характеристического уравнения (77).

Анализ пространства Д параметров.

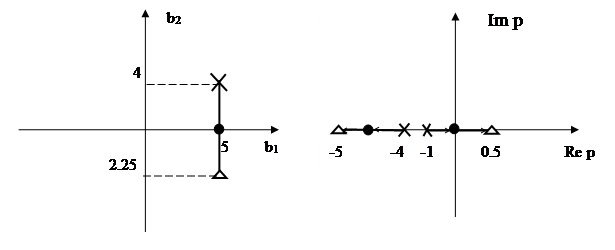Будем изменять непрерывным образом коэффициенты b_i. Точка Т(b₁,…,b_n) при этом непрерывным образом изменяет свое положение в пространстве Д, двигаясь по некоторой кривой. Корни уравнения (77) при этом тоже плавно будут изменять свои величины, вычерчивая на плоскости “p” некоторые кривые, называемые корневыми годографами. Если при изменении коэффициентов b_i точка Т не вышла из области Д_к, то в процессе своего движения корни характеристического уравнения, которые были в левой полуплоскости плоскости “p” останутся там и все корни, которые были в правой полуплоскости плоскости “p” (см. рис.72). Данный рисунок относится к характеристическому уравнению системы второго порядка

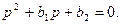
Рис.72.

Здесь поверхностью разделяющей плоскость Д на 3 области Д₀, Д₂, Д₃, является ось абсцисс и положительная полуось ординат. При движении точки Т в области Д₂ по обозначенной кривой корни p₁ , p₂ , изменяют свои значения, но они не попадают в левую полуплоскость плоскости “p”.

Если при изменении значений коэффициентов b_i точка Т вышла из области Д_к, перейдя при этом, например, в область Д_к+1, то это означает, что один из корней характеристического уравнения, бывший раннее в правой полуплоскости, перешел в левую полуплоскость. Если при этом точка Т находится на поверхности, разделяющей области Д_к и Д_к+1, то это означает, что один из корней характеристического уравнения находится на мнимой оси плоскости “p” (см. рис.73).

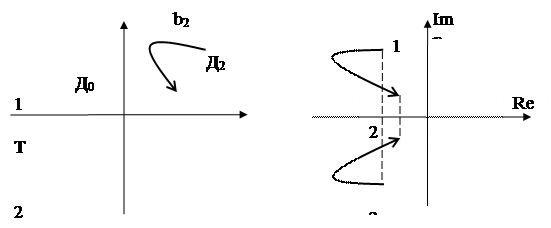Рис.73.

Если при изменении коэффициентов b_i точка Т движется в пространстве Д по поверхности раздела, то это означает, что на мнимой оси плоскости “p” находится какое-то количество (от 1 до n) корней характеристического уравнения (77). Таким образом, поверхность пространства Д, разделяющая его на области Д₀, Д₁,…, Д_n , является отображением мнимой оси плоскости “p”. Следовательно, для получения уравнения данной поверхности необходимо в характеристическом уравнении (77) сделать подстановку p=jω и выбрать коэффициенты b_i так, чтобы уравнение

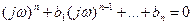(78)

удовлетворялось при всех значениях ω: -∞<ω<+∞. Геометрическое место точек пространства Д, в которых удовлетворяется уравнение (78) будет искомой поверхностью раздела.

Если считать, что в системе высокого (n>3) порядка изменяются все коэффициенты b_i характеристического уравнения, то построение такой поверхности становится крайне затруднительным. Однако задачу определения областей с одинаковым числом левых корней не обязательно решать для всех коэффициентов характеристического уравнения. Эту задачу можно решать относительно определенных параметров системы, например, коэффициента передачи САУ, постоянной времени какого-либо звена и т.п. Это тем более оправдано, что обычно большинство параметров системы является заданными и лишь некоторые параметры можно изменять в определенных пределах.