Критерий Найквиста для астатических систем.

Критерий Найквиста для астатических систем.

Формулировка критерия при этом не меняется, однако поведение годографа W(jw) имеет свои особенности.

Рассмотрим передаточную функцию разомкнутой системы с астатизмом порядка r:

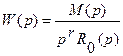
В этом случае

,

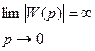годограф W(jw) при w=0 терпит разрыв и аргумент W(jw) при w=0 не определен. Действительно, в данном случае

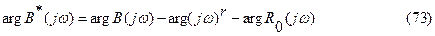
и при w=0 второе слагаемое правой части (73) не определено.

Для устранения неопределенности 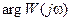следует отнести этот корень либо к левой, либо к правой полуплоскости плоскости “p”. Отнесем корень p=0 к левой полуплоскости. Изменим траекторию движения по плоскости “p”, обходя нулевой корень справа по полуокружности бесконечно малого радиуса (при этом рассматривается изменение w от -¥ до +¥) (см. рис.61).

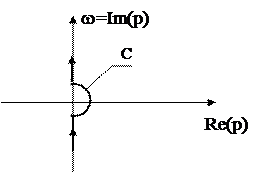Рис.61.

При движении по контуру С, имеем

,

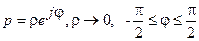так что

Такое изменение движения можно допустить, имея уверенность, что между мнимой осью и контуром С нет нулей ни полинома M(p), ни полинома 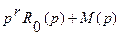. Очевидно, это будет в случае, если радиус r достаточно мал.

Рассмотрим поведение годографа W(jw) при движении на плоскости “p” по контуру С. Имеем

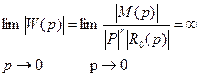
т.е. при движении на плоскости “p” по контуру С модуль АФЧХ бесконечно большая величина. Определим приращение аргумента W(p)

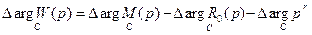
При 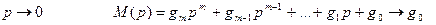и тогда

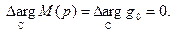
Аналогично .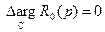

С учетом (74) получим

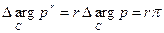
и окончательно можно записать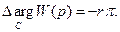

Таким образом, при движении на плоскости “p” по полуокружности С годограф АФЧХ на плоскости “W” может быть представлен точками дуги бесконечно большого радиуса, проходящими путь, соответствующий повороту на угол 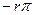, где r – порядок астатизма разомкнутой системы. Случай соответствующий r=1, показан на рис.62. Можно сказать, что

Рис.62

замкнутая система в этом случае устойчива, если характеристическое уравнение разомкнутой САУ не имеет корней в правой полуплоскости плоскости “p”.

На практике, как и для статических систем, обычно строят только половину годографа. При этом годограф W(jω), построенный для значений 0<ω<∞, необходимо дополнить дугой бесконечного радиуса. Эта дуга начинается на положительной полуоси абсцисс, если

Частотный критерий устойчивости по числу пересечений АФЧХ разомкнутой системы вещественной оси на участке - ∞ 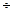- 1.

Повторим критерий Найквиста в следующей формулировке. Если характеристическое уравнение разомкнутой системы имеет e неустойчивых корней, то для того, чтобы была устойчива замкнутая система необходимо и достаточно, чтобы годограф АФЧХ разомкнутой системы W(jω) при изменении ω от 0 до ∞ охватывает точку (-1,j0) e/2 раз.

Обычно W(p) – правильная дробь и при этом 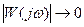при ω →∞ , т.е. годограф W(jω) заканчивается в начале координат плоскости “W”. Тогда о числе охватов можно судить по числу переходов годографа W(jω) через отрезок действительной оси (-∞,-1). Будем считать переход сверху вниз этого отрезка положительным, а снизу вверх – отрицательным. Очевидно, что положительный переход сопровождается увеличением ФЧХ разомкнутой системы, а отрицательный – ее уменьшением. Обозначим общее число положительных переходов через n⁺ , а отрицательных – через n^-. Тогда число охватов годографом W(jω) точки (-1,j0) равно разности между числом положительных и отрицательных переходов этого годографа через отрезок
(-∞,-1) действительной оси и формула (72), выражающая критерий Найквиста, примет вид

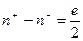(75)

Если при ω=0 годограф начинается на рассматриваемом отрезке, то это считается за ½ перехода. Если разомкнутая система имеет астатизм и пересечение отрезка совершается ее пунктирным дополнением, то это пересечение рассматривается как полноценное и принимается в расчет в формуле (75) .

На рис.63 - 65 показаны примеры годографов АФЧХ разомкнутой САУ. Пусть е=0 , т.е. разомкнутая система устойчива . На рис.63 показан годограф статической системы . Здесь е=0 , n⁺ =2 , n ^- =2 и , таким образом , замкнутая система устойчива .

Рис.63.

На рис.64 представлен годограф АФЧХ разомкнутой системы с астатизмом 3-его порядка. Если е=0, то представленный годограф также отвечает устойчивой в замкнутом виде системе.

Рис.64.

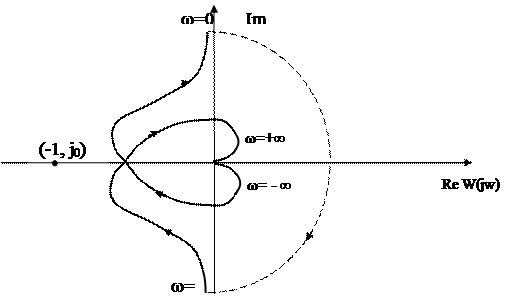
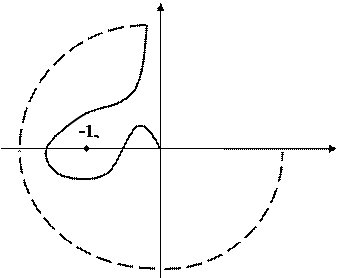
Пусть е=2 и годограф W(jω) имеет вид, представленный на рис. В этом случае n⁺=2, n ^- =1 , условие ( 75) выполняется и замкнутая система устойчива.

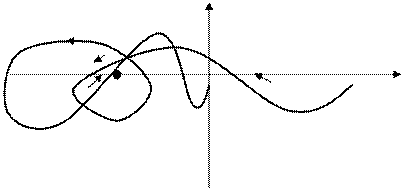Рис.65.