Типовые звенья САУ (продолжение)

Дифференцирующее звено

3.Дифференцирующее звено. Уравнение звена имеет вид

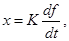
его передаточная функция равна

W(p)=Kp.

АЧХ дифференцирующего звена задается формулой

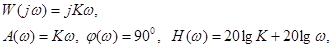
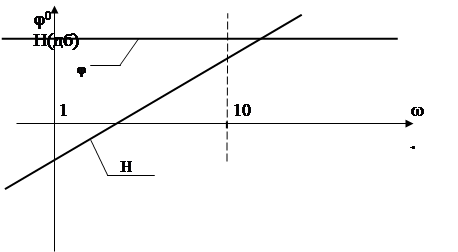т.е. ЛАЧХ представляет собой прямую с наклоном 20 Дб/дек (см. рис.53.)

Рис.53.

Форсирующее звено.

5.Форсирующее звено. Это звено с передаточной функцией

W(p)=K(Tp+1),

где Т – постоянная времени, К – коэффициент передачи звена .

Частотные характеристики форсирующего звена :

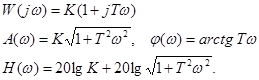
Вводя асимптоты ЛАЧХ аналогично тому, как это было сделано для апериодического звена, получим, что низкочастотная асимптота определяется выражением H(w)=20lgK, (соответствующий график представляет собой горизонтальную линию ), а высокочастотная выражением

H(w)=20lgK+20lgT+20lgw .

(на графике это прямая с наклоном +20 Дб/дек).

Как и ранее, эти асимптоты пересекаются при w=1/T – частота сопряжения звена. Для построения φ(w) используется тот же шаблон , что и для апериодического звена . Вид ЛАФЧХ форсирующего звена показан на рис. 54.

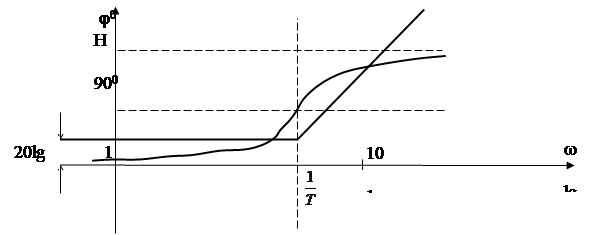Рис.54.

Колебательное звено.

6.Колебательное звено. Дифференциальное уравнение этого звена имеет вид

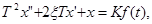
величина Т называется постоянной времени , 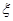- коэффициент затухания , К – коэффициент передачи звена . Передаточная функция определиться выражением

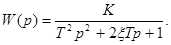(50)

Заметим , что при постоянном входном сигнале f(t)=B 1(t) вынужденное движение имеет вид

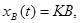
т.е. происходит умножение входного сигнала на коэффициент передачи .

В передаточной функции (50) принимается ξ<1. При этом характеристический многочлен имеет пару комплексно-сопряженных корней . При ξ>1 корни действительные и передаточная функция (50) может быть сведена к произведению 2-х передаточных функций , каждая из которых соответствует апериодическому звену .

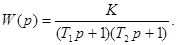
АФЧХ колебательного звена определится выражением

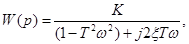
откуда

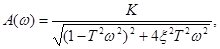
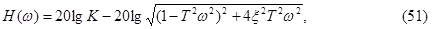
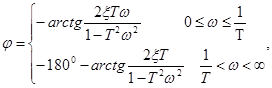
Из формулы (51) видно, что при малых w

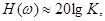
а при больших значениях w

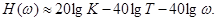
Отсюда следует, что ЛАЧХ колебательного звена имеет асимптоты : низкочастотную горизонтальную и высокочастотную с наклоном – 40 дб/дек . Эти асимптоты пересекаются при w=1/T – сопрягающей частоте колебательного звена . Поправки к асимптотической ЛАЧХ , доводящие ее до полной характеристики , зависят от коэффициента затухания ξ..

ЛАФЧХ колебательного звена при К=1, Т=1с,показаны на рис.55.

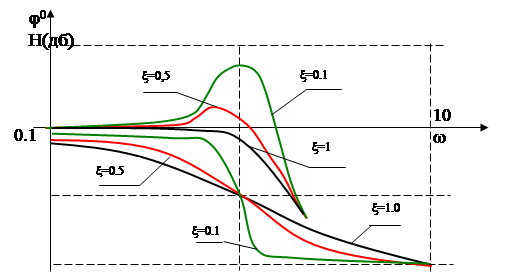Рис.55

ЛАФЧХ изменяется от 0 до – 180⁰ и является монотонно убывающей функцией. ЛАЧХ может иметь резонансный пик. Этот пик будет существовать при ξ<0,707 . Высота пика характеристики A(w) определяется формулой

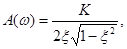
т.е. она тем больше , чем меньше коэффициент затухания . При этом

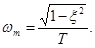
Импульсная переходная функция колебательного звена имеет вид

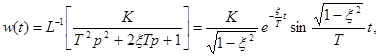
а переходная характеристика определяется формулой

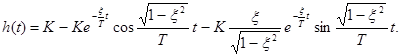
Частным случаем колебательного звена , соответствующим ξ=0 , является консервативное с передаточной функцией

.

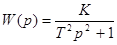Временные характеристики консервативного звена, соответствуют незатухающим колебаниям с круговой частотой w=1/T .

АФЧХ определяются зависимостями

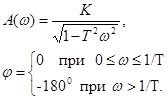
Форсирующее звено 2-ого порядка.

7. Форсирующее звено 2-ого порядка. Передаточная функция звена имеет вид

Рассмотрение ЛАФЧХ этого звена проводится аналогично колебательному звену. ЛАЧХ имеет 2 асимптоты : низкочастотную горизонтальную

H(w)=20lgK

и высокочастотную с наклоном + 40 дб/дек :

H(w)=20lgK+40lgw+40lgT.

Для перехода от асимптотических ЛАФЧХ к полным характеристикам используются те же шаблоны поправок , что и для колебательного звена , но с обратными знаками . Фазовые характеристики этого звена определяются соотношениями

т.е. они противоположны ЛФЧХ колебательного звена.

Неустойчивые и не минимально-фазовые звенья.

Это звенья с передаточными функциями

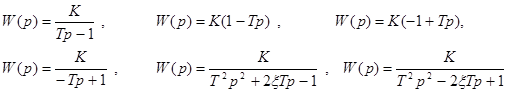
и т.д.

ЛАФЧХ всех этих звеньев необходимо уметь строить.

Кроме рассмотренных выше звеньев рассмотрим еще звено с запаздыванием. Это звено , поведение которого определяется уравнением

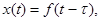
где τ – время запаздывания. Передаточная функция этого звена определится выражением

W(p)=e^-pτ ,

откуда следует , что

A(w)=1 , φ(w)= -wτ .