Частотные критерии устойчивости.

Частотные критерии устойчивости (общие положения).

Частотные критерии устойчивости основаны на определении условия отрицательности вещественных корней характеристического уравнения системы по виду ее частотных характеристик.

В 1932 г. для исследования элементарных усилителей с отрицательной обратной связью Найквист использовал частотные характеристики усилителя с разомкнутой обратной связью. Им был дан критерий устойчивости усилителя по виду АФЧХ этого усилителя с разомкнутой обратной связью.

В статье “Метод гармонического анализа в теории автоматического регулирования”, опубликованной в журнале “Автоматика и телемеханика” в 1963 г. А.В.Михайлов обосновал и впервые применил частотные методы для исследования систем автоматического управления.

Основное преимущество частотных методов заключается в их наглядности. Задача оценки устойчивости сводится к изучению некоторой плоской кривой, которая может быть получена аналитически или экспериментально. Важно, что при экспериментальном построении частотных характеристик становится возможной оценка устойчивости системы, дифференциальные уравнения которой неизвестны.

Критерий устойчивости Михайлова.

Рассмотрим характеристический многочлен системы

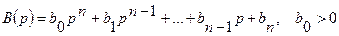
Обозначим его корни p₁,p₂,…,p_n. Тогда многочлен B(p) можно представить в виде

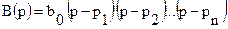
Подставим в B(p) p=jw. Получим

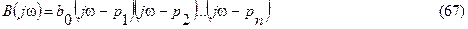
B(jw)-комплексная функция действительного переменного w:

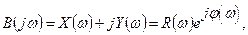
при этом X(w)- четная функция w, Y(w)- нечетная функция w, т.е.

.

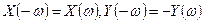При изменении w от -¥ до +¥ на комплексной плоскости “B” точка B(jw) перемещается по некоторой кривой, называемой годографом Михайлова. При этом годограф Михайлова симметричен относительно оси абсцисс.

Рассмотрим, как изменяется величина j(w) (аргумент B(jw)) при изменении w от -¥ до +¥. Выясним, как изменяется аргумент jw-p_i при изменении w в указанных пределах. Соответствующие векторы p_i, jw, jw-p_i показаны на рисунке 57.

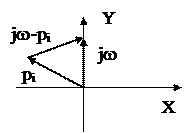Рис.57

Из рисунка видно, что, если 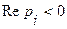, то

-¥ <w< +¥

а, если 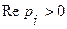, то

-¥ <w< +¥

В устойчивой системе m=0 и тогда

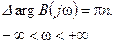
При построении годографа Михайлова можно ограничиться его половиной, соответствующей w: 0 <w< +¥. При этом часть годографа, соответствующая w:

-¥ <w<0 будет представлять собой зеркальное отображение построенной таким образом кривой относительно действительной оси.

Изменению w от 0 до ¥ соответствует половина общего приращения аргумента, т.е.

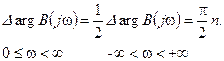
Критерий Михайлова: Для устойчивости автоматической системы n-го порядка необходимо и достаточно, чтобы вектор B(jw), определяющий годограф Михайлова при изменении w от 0 до ¥ поворачивается на угол 0.5pn.

В случае, если характеристическое уравнение имеет корни jw₀ на мнимой оси (граничный случай),

,

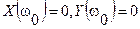т.е. при данном значении w годограф B(jw) проходит через начало координат комплексной плоскости “B”.

Критерий Михайлова может быть сформулирован по-другому.

Очевидно, что приращение аргумента на 0.5p соответствует прохождению годографом Михайлова одного квадранта в положительном направлении. Столь же очевидно, что B(0)=b_n>0 (в противном случае имеется как минимум один вещественный неустойчивый корень). С учетом сказанного можно утверждать, что необходимым и достаточным условием устойчивости линейной системы будет последовательное прохождение годографом Михайлова при изменении w от 0 до ¥ n квадрантов в положительном направлении, начиная с положительной вещественной полуоси.

Критерий устойчивости Найквиста.

Рассмотрим замкнутую систему с единичной обратной связью. Структурная схема системы показана на рисунке 58.

Рис.58

Частотный критерий Найквиста позволяет судить об устойчивости или неустойчивости замкнутой САУ по АФЧХ соответствующей разомкнутой системы.

Сделаем несколько замечаний.

1.Передаточная функция разомкнутой системы как правило представляет собой правильную дробь, т.е.

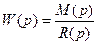
и степень полинома M(p) меньше степени полинома R(p).

2.Порядок замкнутой и разомкнутой системы совпадают. Действительно, для замкнутой системы имеем

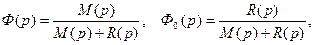
во всех случаях характеристический многочлен замкнутой системы имеет вид

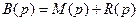
и его степень равна степени полинома R(p).

Пусть замкнутая система находится на границе устойчивости, т.е. имеем корни, находящиеся на мнимой оси p₁₂= ±jw₁. Тогда

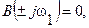
откуда

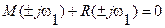
и

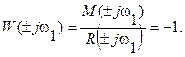
Таким образом, если годограф вектора W(jw) при изменении w от -¥ до +¥ пересекает действительную ось в точке (-1,j0) при некотором w, то замкнутая система находится на границе устойчивости. Иначе говоря, если годограф B(jw) пройдет через начало координат, то годограф W(jw) пройдет через точку (-1,j0). Поэтому точка (-1,j0) на плоскости “W” является аналогией начала координат плоскости “B”. Это обстоятельство позволяет проверить устойчивость замкнутой системы по АФЧХ разомкнутой системы W(jw) при различных w.

Рассмотрим изменение аргумента функции

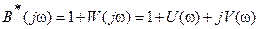
При изменении w от -¥ до +¥. Характеристику B^*(jw) можно представить в виде

,

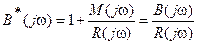Где B(jw) – характеристический многочлен замкнутой системы,

R(jw) – характеристический многочлен разомкнутой системы.

Тогда

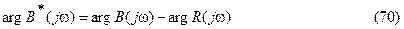
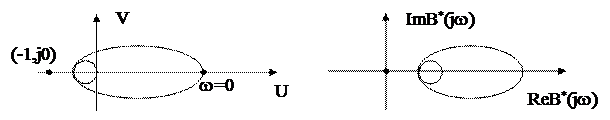Качественный вид годографов W(jw), B^*(jw) приведен на рисунке.59

Рис.59.

Далее рассмотрим отдельно случай, когда передаточная функция разомкнутой системы W(p) имеет полюсы (корни характеристического уравнения) на мнимой оси и случай, когда такие полюсы отсутствуют.

1.Передаточная функция W(p) не имеет полюсов на мнимой оси. Тогда все корни характеристического уравнения разомкнутой системы R(p)=0 могут принадлежать левой полуплоскости плоскости “p” (разомкнутая система устойчива) или некоторые из этих корней могут находиться в правой полуплоскости (разомкнутая система неустойчива).

1.1.Пусть разомкнутая система устойчива. Тогда из критерия Михайлова

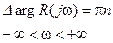
Если устойчива замкнутая система, то

.

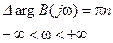Следовательно, замкнутая система устойчива, если

.

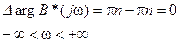Это означает, что годограф вектора B^*(jw) не охватывает начало координат плоскости “B” или, что то же самое, годограф вектора W(jw) не охватывает на комплексной плоскости “W” точку (-1,j0).

При использовании этого критерия строят годограф АФЧХ разомкнутой системы

,

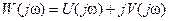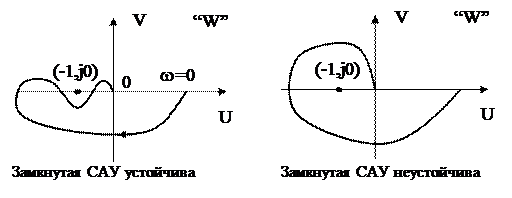при этом можно рассматривать только значения w в диапазоне 0£w£¥ и проверяют, охватывает ли этот годограф точку (-1,j0). Примеры годографов W(jw), соответствующих устойчивой и неустойчивой в замкнутом состоянии системам, преведены на рисунке 60.

Рис.60.

1.2.Пусть характеристическое уравнение имеет l неустойчивых корней. Тогда

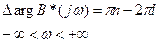
и следовательно, замкнутая система устойчива, когда

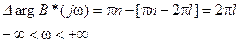
Для этого случая критерий устойчивости Найквиста можно сформулировать следующим образом: САУ, неустойчивая в разомкнутом состоянии, устойчива в замкнутом состоянии, если АФЧХ разомкнутой системы W(jw) при изменении w от -¥ до +¥ охватывает точку (-1,j0) комплексной плоскости “W” l раз, где l - количество неустойчивых корней разомкнутой системы.

Приведенной формулировке соответствует условие

где 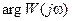отсчитывается относительно точки (-1,j0). Как и в первом случае можно ограничиться половинным диапазоном изменения w: 0<w<¥, тогда условие (71) переходит в условие