Типовые звенья САУ.

Статические и динамические звенья.

При исследовании САУ они обычно разбиваются на отдельные звенья . Звенья , входящие в САУ , могут быть статическими и динамическими . Статические звенья – это звенья, у которых связь между входной x_вх и выходной x координатой определяется алгебраическим уравнением

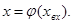
Если функция 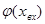линейна , т.е. x=k* x_вх ,

то такое статическое звено является линейным . Во всех остальных случаях оно не линейно .

Динамические звенья – это звенья , у которых связь между выходом и входом звена описывается дифференциальным уравнением .В нашем курсе – это линейное дифференциальное уравнение с постоянными коэффициентами .

Передаточная функции линейных САУ представляют собой дробно-рациональные функции переменной “p” с действительными коэффициентами . Такие полиномы (как в числителе , так и в знаменателе ) имеют действительные или комплексно-сопряженные корни . При разложении полиномов на элементарные множители действительный корень дает сомножитель в виде линейного двучлена , а пара комплексно-сопряженных корней – сомножитель в виде квадратного трехчлена относительно “p”. Нулевой корень даст дополнительный сомножитель p . Следовательно , передаточная функция любой стационарной линейной системы может быть сведена к произведению некоторых передаточных функций . В этих элементарных передаточных функциях максимальная степень p не превышает двух . Звенья , соответствующие этим передаточным функциям , назовем типовыми .

Рассмотрим типовые звенья их уравнения и характеристики.

Безынерционное (усилительное) звено.

1.Безынерционное (усилительное) звено.

Уравнение звена

x=k*f ,

где х – входная , f – выходная переменные .

Передаточная функция

W(p)=k,

Переходная функция

h(t)=k 1(t)

Весовая характеристика w(t)=kδ(t).

АЧХ звена W(jw)=k , откуда получаем

ЛАЧХ H(w)=20lg k , φ(w)=0 (см. рис.47)

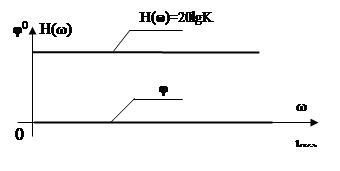Рис.47

Интегрирующее звено.

2.Интегрирующее звено. Оно описывается уравнением

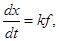
откуда

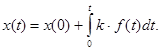
Передаточная функция звена имеет вид

.

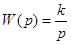Переходная характеристика h(t) и импульсная переходная функция w(t) определяется выражениями

h(t)=kt ,

w(t)=k 1(t).

АЧХ интегрирующего звена задается формулой

W(jw)=k / jw ,

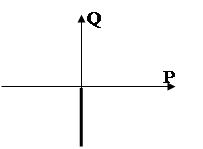откуда следует, что P(w)=0 , Q(w)= - k / w , A(w)= k / w , φ(w)=-90⁰.Годограф АЧХ на комплексной плоскости на рис.48.

Рис.48.

ЛАЧХ звена имеет вид

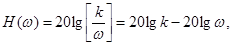
т.е. ЛАЧХ интегрирующего звена представляет собой с отрицательным наклоном

20 Дб / дек , принимающую при lgw=0 (w=1) значение 20 lg k . Фазовая характеристика интегрирующего звена представляет собой прямую φ= - 90⁰ (см.рис. 49).

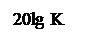Рис.49.

Апериодическое звено.

3.Апериодическое звено. Это звено , передаточная функция которого имеет вид

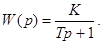(45)

здесь К – коэффициент передачи , Т – постоянная времени апериодического звена. К такому виду может быть также приведена передаточная функция

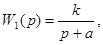
а именно

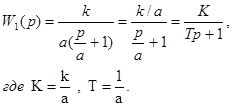
Передаточная функция (45) соответствует следующее дифференциальное уравнение :

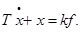
Его решение при f(t)=1(t) и нулевом начальном условии x(0)=0 дает переходную характеристику

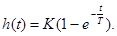(46)

График h(t) показан на рис.50.

Рис.50.

Из зависимости (46) видно , что установившиеся значение выходного сигнала при единичном ступенчатом входном воздействии равно К . Время регулирования , определяемое по моменту входа в 5% отклонение от установившегося значения составляет 3Т

t_p=3T .

Импульсная переходная функция звена получается как обратное преобразование Лапласа его передаточной функции , т.е.

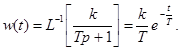
Для определения частотной характеристики положим p=jw . Тогда

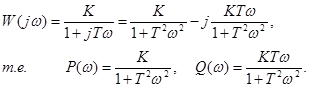
Формулы для АЧХ и ФЧХ имеют вид

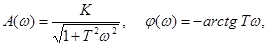
а для ЛАЧХ – вид

(47)

На рис.51. Представлен годограф АЧХ апериодического звена, соответствующий изменению w от 0 до ∞ (к>0, T>0). Он представляет собой полуокружность радиуса к/2 c центром в точке (k/2, 0)

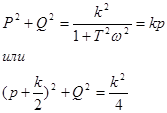
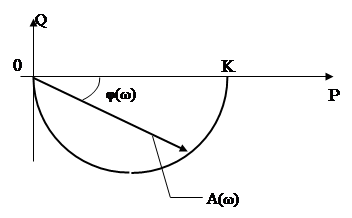Рис.51.

Из (47) следует , что при очень малых частотах (w 0)

H(w)=20lgK , (48)

а при очень больших частотах, когда можно принять , что

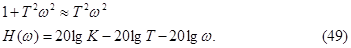
Зависимость (48) определяет горизонтальную прямую, а зависимость (49) – прямую с наклоном – 20 дб/дек. Первая прямая называется асимптотой в области низких частот, а вторая асимптотой в области высоких частот. Они пересекаются при частоте w=1/T, которая называется сопрягающей частотой звена. ЛАЧХ звена, получающаяся заменой характеристики (47) двумя асимптотами (48), (49) называется асимптотической ЛАЧХ. При этом максимальная ошибка составляет она получается при w=1/T. Вид ЛАЧХ апериодического звена показан на рис. 51. Для построения ЛФЧХ φ(w) может использоваться шаблон .

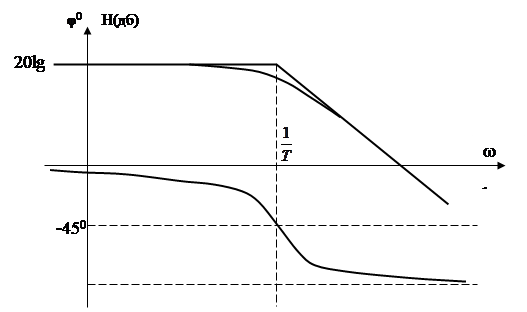Рис.52.