Частотные характеристики линейных САУ.

Частотные характеристики линейных САУ.

Рассмотрим прохождение гармонического сигнала f(t)=Acoswt через САУ с передаточной функцией W(p) и найдем установившуюся реакцию системы на этот входной сигнал.

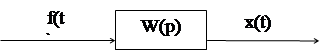Рис.43.

Для упрощения выкладок введем сигнал 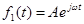и найдем установившуюся реакцию x₁(t) на этот сигнал. Тогда по принципу суперпозиции , так как

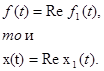
Итак , определим реакцию системы на сигнал f₁(t). С использованием преобразования Лапласса получим

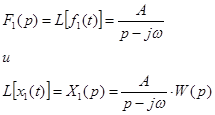
Положим для простоты , что все корни p₁ ,p₂, …,p_n характеристического многочлена системы простые и

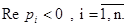(41)

Обозначим W(p)=B(p)/D(p). Тогда с использованием формул обратного преобразования Лапласа найдем

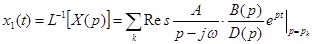(42)

В формуле (42) P_k особые точки выражения , стоящего под знаком вычета. Это точка p₀=jw и значение p_i , i= 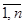- корни характеристического многочлена системы D(p). Из (42) с использованием формул вычетов найдем

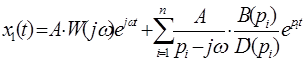
С учетом (41) получим , что

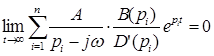
т.е. установившаяся реакция системы на сигнал f₁(t) имеет вид

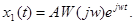
Выделяя действительную часть последнего выражения , получим установившуюся реакцию на сигнал f(t) :

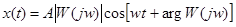
или

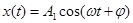, (43)

где

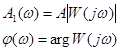(44)

Из анализа (43), (44) можно сделать следующие выводы :

1. Установившаяся реакция ( в общем случая вынужденный процесс ) линейной системы на гармонический входной сигнал представляет собой гармонический сигнал той же частоты.

2.При этом амплитуда гармонического сигнала на выходе отличается от амплитуды гармонического входного сигнала в 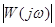раз.

3.Фаза гармонического выходного сигнала отличается от фазы входного сигнала на величину argW(jw) ;

Выражение

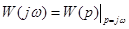
получающегося подстановкой в передаточную функцию W(p), называется амплитудно-фазовой частотной характеристикой (АФЧХ) линейной системы , или просто частотной характеристикой САУ.

АФЧХ системы представляет собой преобразование Фурье импульсной переходной характеристики (весовой функции) w(t), т.е.

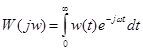
(при постановке проделав интегрирование учтено, что )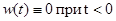

АФЧХ W(jw) является комплексной функцией вещественного переменного w и она может быть представлена в следующем виде :

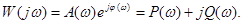
В этом выражении

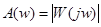- амплитудная частотная характеристика (АЧХ),

φ(w)=arg W(jw) – фазовая частотная характеристика (ФЧХ),

P(w)=Re W(jw) – вещественная частотная характеристика,

Q(w)=Im W(jw) – мнимая частотная характеристика.

Таким образом , система может быть задана либо характеристиками A(w), φ(w) либо характеристиками P(w), Q(w)

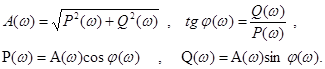
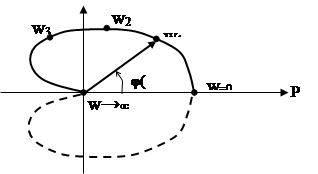Для наглядного представления АФЧХ W(jw) используется комплексная плоскость. Для каждого значения w находится соответствующая точка W(jw)=P(w)+jQ(w) на комплексной плоскости. При непрерывном изменении частоты w от 0 до ∞ положение изображающей точки на комплексной плоскости меняется непрерывным образом. Геометрическое место точек, соответствующих значениям w от 0 до ∞ представляет собой годограф амплитудно-фазовой частотной характеристики (см. рис.44)

Рис.44.

АФЧХ может быть построена как для положительных, так и для отрицательных частот. При замене w на –w получим

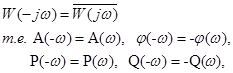
в итоге АФЧХ для отрицательных частот получается зеркальным отображением АФЧХ для положительных частот относительно оси абсцисс комплексной плоскости.

В принципе можно ограничиться рассмотрением только положительных частот. Однако при использовании всего диапазона частот -∞ <w<+∞ многие формулы получают более удобный вид.

На практике наиболее часто используется амплитудная и фазовая частотные характеристики A(w), φ(w). При этом используются соответствующие графики в функции w (см. рис.45)

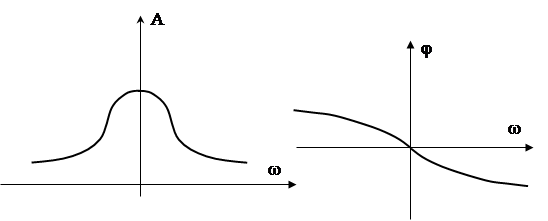Рис.45.

Минимально-фазовые звенья и системы.

Если все нули и полюсы передаточной функции W(p) левые, т.е. лежат в левой полуплоскости комплексной плоскости “p”, то звено стакой передаточной функцией называется минимально-фазовой . Звено не удовлетворяющее этому свойству , называется не минимально-фазовым. Минимально-фазовые звенья имеют меньшие по абсолютной величине фазовые характеристики по сравнению с звеньями не минимально-фазовыми.

Для минимально-фазовых звеньев имеют место следующие зависимости :

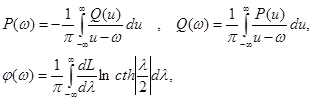
где L(u)=lnA(u), λ=ln u/w, u – переменная интегрирования.

Эти зависимости показывают, что для минимально-фазовых звеньев достаточно задаться характеристикой P(w) или Q(w) или A(w). Поэтому при рассмотрении таких систем можно ограничиться, например, АЧХ A(w).Фазовая характеристика при этом полностью определяется АЧХ.

Логарифмические частотные характеристики.

В инженерной практике наибольшее распространение получили логарифмические амплитудно-фазовые частотные характеристики (ЛАЧХ) САУ. Это характеристики имеющие следующие особенности :

1.Рассматривается логарифмическая амплитудно-фазовая частотная характеристика (ЛАЧХ) H(w) и логарифмическая фазовая характеристика (ЛФЧХ) φ(w) системы. При этом по оси w (оси абсцисс) используется логарифмический масштаб (см. рис.46.) Отрезок, соответствующий 10-кратному изменению частоты, называется декадой. Обычно в построениях 1 декада соответствует 50 мм.

Рис.46.

2.Амплитудано-частотная характеристика заменяется логарифмической амплитудно- частотной характеристикой по формуле

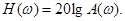
Эта величина измеряется в децибелах (дБ) . Если A(w)=1 , то H(w)=0 дБ,

A(w)=10 соответствует H(w)=20 дБ ,

A(w)=100 соответствует H(w)=40 дБ ,

A(w)=0.1 соответствует H(w)= -20 дБ и т.д. Заметим также, что

A(w)=2 соответствует (примерно) 6 дБ и

A(w)=1.41 соответствует H(w) 3 дБ .

При построении ЛАЧХ по оси ординат откладывают значения H(w) в дБ. В стандартной сетке 1 дБ соответствует 2 мм. Ось абсцисс проходит через значение H(w)=0 . Ось ординат располагается достаточно произвольно, обычно ее расположение определяется параметрами системы.

3.ЛФЧХ строится в координатах φ - lg w , т.е. сама характеристика φ(w) преобразованиям не подвергается . В стандартной сетке 1⁰ соответствует 1мм.

Достоинством ЛАЧХ является их наглядность и возможность построения практически без вычислительной работы . Особенно это проявляется , когда АФЧХ является произведением отдельных сомножителей . Пусть, например

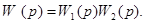
Тогда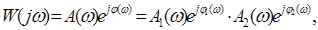

т.е.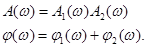

При этом ЛАЧХ соединения определяется выражением.

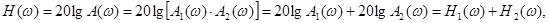
т.е. ЛАЧХ последовательного соединения равна сумме ЛАЧХ входящих в него звеньев. Так как фазовые характеристики в этом случае также суммируются, то определение результирующих ЛАЧХ сводится к простейшим построениям.