Временные характеристики САУ.
Временные характеристики САУ.
Ранее для описания динамических свойств САУ и их элементов использовались дифференциальные уравнения и передаточные функции. Динамические свойства звеньев могут быть также определены по его переходной функции ( переходной характеристики ) и импульсной переходной функции ((весовой функции), (функции веса)).
Переходная функция системы (звена) представляет собой переходный процесс на выходе , возникающий при подаче на вход единичной ступенчатой функции 1(t) при нулевых начальных условиях. Стандартные обозначения переходной функции h(t) (см. рис.41)
 |
Рис.41.
Если входное воздействие представляет собой запаздывающую единичную ступенчатую функцию, f(t)=1(t - a), то при нулевых начальных условиях на выходе будет наблюдаться реакция h(t-a), a = const .
Импульсная переходная функция системы или звена представляет собой переходный процесс на выходе , возникающий при подаче на вход δ – функции при нулевых начальных условиях . Она обозначается как w(t) (см. рис.42)
 |
Рис.42.
Связь между переходной характеристикой и импульсной переходной функцией.
Установим связь между переходной характеристикой и импульсной переходной функцией . Рассмотрим дифференциальное уравнение звена
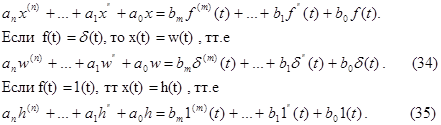
Продифференцируем однократно последнее неравенство . Получим
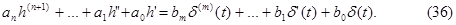
Сравнивая (34) и (36), найдем
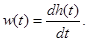 (37)
(37)
Отметим, что h(t) 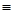 0 при t<0 , w(t)
0 при t<0 , w(t) 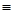 0 при t<0 . Это следует , в частности , из физических соображений : следствие не может появиться раньше причины . В общем случае
0 при t<0 . Это следует , в частности , из физических соображений : следствие не может появиться раньше причины . В общем случае 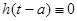 при t<a , w(t-a)
при t<a , w(t-a) 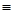 0 , при t<a.
0 , при t<a.
Таким образом помимо дифференциального уравнения для описания одного и того же звена можно использовать :
- передаточную функцию W(p) ,
- переходную характеристику h(t),
- импульсную переходную функцию w(t).
Связь между h(t) и w(t) задается выражением (37). Установим связь между w(t) и W(t), а также между h(t) и W(p).
Уравнение звена в изображениях имеет вид
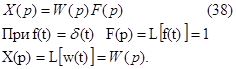
Таким образом
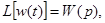
т.е. преобразование Лапласа импульсной переходной функцией звена представляет собой переходную функцию того же звена .
Пусть f(t)=1(t). Тогда F(p)=1/p и из (38) получим
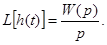
Пример. Пусть 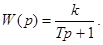 Найдем импульсную переходную функцию и переходную характеристику этого звена .
Найдем импульсную переходную функцию и переходную характеристику этого звена .
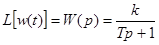
и тогда
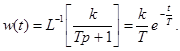
Для переходной характеристики получим
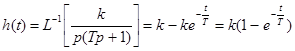 .
.
Интегральная связь выходной координаты с входной.
Рассмотрим определение выходной координаты звена или системы при произвольном входном воздействии f(t) . Звено имеет передаточную функцию W(p) , импульсную переходную функцию w(t) и переходную характеристику h(t).
Запишем уравнение звена в изображениях
X(p)=F(p) W(p).
По теореме свертки во временной области
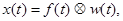
Где f(t) – оригинал , соответствующий изображению F(p) , т.е. входной сигнал ; w(t) – оригинал , соответствующий изображению W(p) , т.е. импульсная переходная функция.
Таким образом
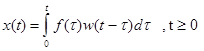 (39)
(39)
или с учетом свойства коммутативности свертки

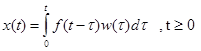
При этом 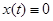 при t<0 . Это следует , например , из (39) . В этом выражении
при t<0 . Это следует , например , из (39) . В этом выражении 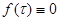 при
при 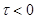 , т.е.
, т.е.
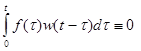 при t<0 .
при t<0 .
Пример . Пусть уравнение САУ имеет вид
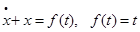
Определить выходную координату системы.
Находим импульсную переходную функцию , т.е. решение уравнения
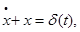
С помощью преобразования Лапласа имеем
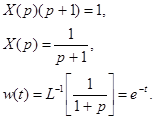
С использованием зависимости (39) найдем
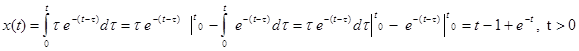
Получим интегральную связь , выражающую выходной сигнал через входной с помощью переходной характеристики . Обозначим
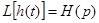

Тогда из (38) имеем

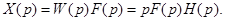 (39)
(39)
По теореме об изображении производной
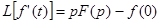
отсюда следует, что
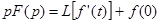 (40)
(40)
Объединяя (39), (40), можно записать
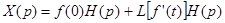
после чего, переходя к оригиналам, с учетом теоремы свертки получим
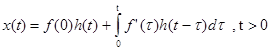 (41)
(41)
Применение формулы (41) для предыдущего примера дает следующий результат :
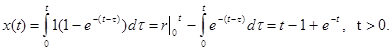
| <== предыдущая лекция | | | следующая лекция ==> |
| Передаточные функции различных систем. | | | Понятие базы данных и системы баз данных |
Дата добавления: 2017-10-04; просмотров: 2898;











