Алгоритм решения задач с помощью теоремы об изменении количества движения СМТ – схема
Алгоритма Д43 КДС с комментариями и примерами
Комментарии
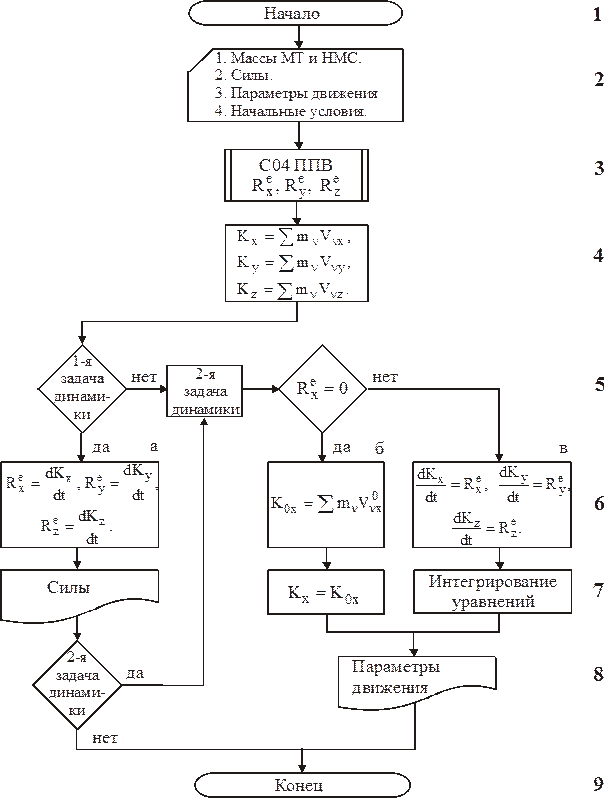
К.2. Рассматриваемый объект принимается за МС, указывается система отсчета, в которой исследуется ее движение. Выделяются МТ и НМС, входящие в МС. На чертеже изображается силовая схема, т. е. рисуются все внешние силы, действующие на МС, в том числе внешние пассивные силы – силы реакции связи на основании принципа освобождаемости от связей (аксиома 5 статики). Определяются начальные условия.
К.3,4. Находятся проекции главного вектора внешних сил и количество движения МС только на те направления (оси), вдоль которых необходимо определить силы (первая задача динамики) и перемещения или кинематические параметры (вторая задача динамики).
Количество движения МС определяется для текущего или заданного момента времени. Все скорости выражаются либо через те, которые заданы, либо через те, которые необходимо определить. В случае сложного движения МТ, входящей в МС, в формуле для ее количества движения должна быть взята абсолютная скорость – 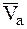 (Ч.1 Кинематика, схема алгоритма К07 СДТ).
(Ч.1 Кинематика, схема алгоритма К07 СДТ).
К.5б.Для случая 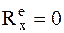 ось х выбрана для определенности. В реальной задаче такой осью может быть любая другая.
ось х выбрана для определенности. В реальной задаче такой осью может быть любая другая.
К.7в.При интегрировании используются либо метод разделения переменных, либо теория линейных дифференциальных уравнений первого и второго порядка. Постоянные интегрирования находятся с помощью начальных условий.
Примечание
Теорема об изменении количества движения МС чаще всего применяется в случаях, когда НМС совершает поступательное движение, а МТ – любое движение, для определения перемещений того или иного объекта и для определения изменения скоростей МТ или НМС.
Пример 1
2 По наклонной поверхности платформы массы m1, движущейся в начальный момент времени со скоростью V0, начинает перемещаться тележка массы m2, с относительной скоростью Vr = u (2 – t) (рис. 30). Определить полную реакцию колес платформы (N = N1 + N2) и скорость платформы V в момент времени t = 1 c (трением при движении платформы и тележки пренебречь).
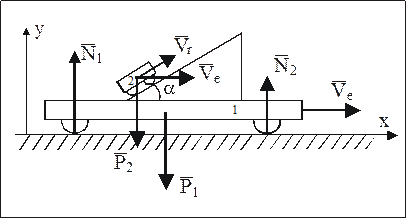
Рис. 30
МС состоит из платформы – АТТ и тележки – МТ, совершающей сложное движение с относительной скоростью 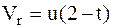 и переносной скоростью
и переносной скоростью  .
.
Для определения полной реакции N (первая задача динамики) все соотношения для текущего момента времени проектируются на ось у.
Для определения скорости 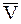 (вторая задача динамики) все соотношения для начального и конечного моментов времени проектируются на ось х.
(вторая задача динамики) все соотношения для начального и конечного моментов времени проектируются на ось х.
|
 3
3
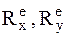
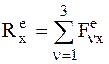 = 0,
= 0,
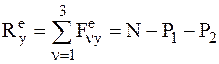 .
.
4 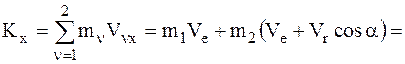
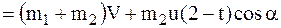 .
.
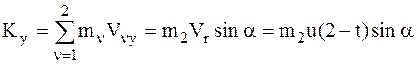 .
.
5 1-я задача динамики,
6а 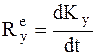 ®
® 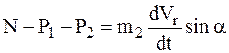 .
.
7а 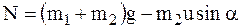
 .
.
5 2-я задача динамики, 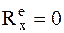 .
.
6б 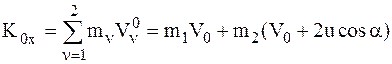
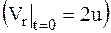 .
.
7б 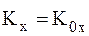 ,
,
(m1+ m2)V + m2u(2 – t)cos a = (m1 + m2)V0 +2 m2u cos a.
8 Ответ: 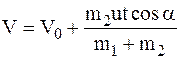
Дата добавления: 2016-06-05; просмотров: 2500;











