Кинетического момента СМТ

Запишем теорему об изменении момента количества движения МТ (1.34) для n-й точки СМТ, учтя, что на нее действуют 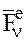– равнодействующая всех внешних сил и 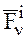– равнодействующая всех внутренних сил:

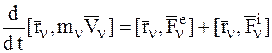. (n=1,2,...,n)

Просуммировав эти выражения и учитывая, что сумма производных равна производной от суммы, получим:

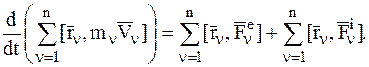(4.21)

Используя формулу для главного момента системы сил (Ч.2 Статика) и учтя свойство внутренних сил – соотношение (3.3), имеем:

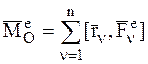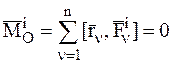, , (4.22)

где 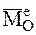- главный момент всех внешних сил, а 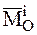- главный момент всех внутренних сил относительно какого-либо центра.

Введем понятие кинетического момента СМТ относительно какого-либо центра О.

Определение: Кинетическим моментом или моментом количества движения СМТ называется геометрическая сумма моментов количества движения МТ, входящих в СМТ, относительно того же центра:

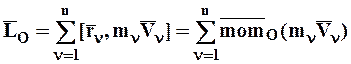. (4.23)

Подставив (4.22) и (4.23) в (4.21), получим теорему об изменении кинетического момента СМТ в следующем виде:

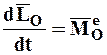. (4.24)

Теорема: Производная по времени от кинетического момента СМТ относительно какого-либо центра равна главному моменту всех внешних сил, действующих на СМТ, относительно того же центра.

Спроектировав соотношения (4.24) на оси декартовой системы координат с началом в центре О и учтя связь между моментами силы относительно точки и оси, получим:

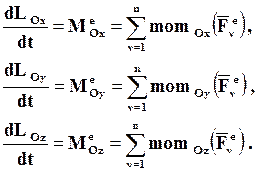(4.25)

Отсюда следует, что производная по времени от проекции кинетического момента СМТ на какую-либо ось равна проекции главного момента всех внешних сил, действующих на СМТ, на эту ось или сумме моментов всех внешних сил, действующих на СМТ, относительно этой оси.

Следствия:

· Если 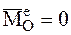, то из соотношения (4.24) следует, что

.

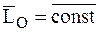Если главный момент внешних сил, действующих на СМТ, относительно какого-либо центра равен нулю, то кинетический момент СМТ относительно того же центра постоянен по величинеи направлению и равен кинетическому моменту СМТ относительно того же центра в начальный момент времени:

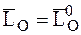. (4.26)

Соотношение (4.26) выражает закон сохранения кинетического момента для СМТ.

· Если 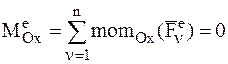(для определенности выбрана ось х), то из первого соотношения (4.25) следует, что

.

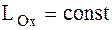Если проекция главного момента всех внешних сил, действующих на СМТ, на какую-либо ось (сумма моментов всех внешних сил относительно какой-либо оси) равна нулю, то проекция кинетического момента на эту ось является постоянной величиной и равняется проекции кинетического момента на эту ось в начальный момент времени

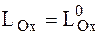. (4.27)

Найдем кинетический момент НМС, вращающейся относительно неподвижной оси Оz (рис. 33)

.

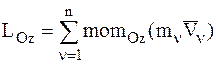Скорость n-й точки НМС, вращающейся относительно неподвижной оси, определится соотношением (Ч.1 Кинематика):

,

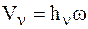где w – угловая скорость НМС, а h_n – расстояние от n-й точки НМС до оси z.

Момент количества движения n-й МТ относительно оси Oz примет вид:

.

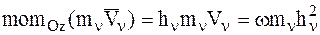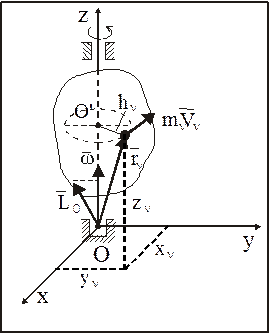
Рис. 33

Тогда кинетический момент НМС относительно неподвижной оси определится из соотношения:

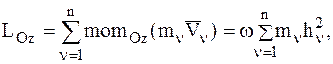
здесь 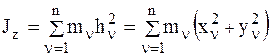– момент инерции НМС относительно оси Oz.

Итак, для кинетического момента НМС, вращающейся относительно неподвижной оси, получим:

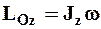. (4.28)

Величина кинетического момента НМС, вращающейся относительно неподвижной оси, равна произведению момента инерции НМС относительно той же оси на угловую скорость НМС (4.28).

4.7. Алгоритм решения задач с помощью теоремы об изменении кинетического момента СМТ – схема алгоритма Д47 КМС с комментариями и примерами

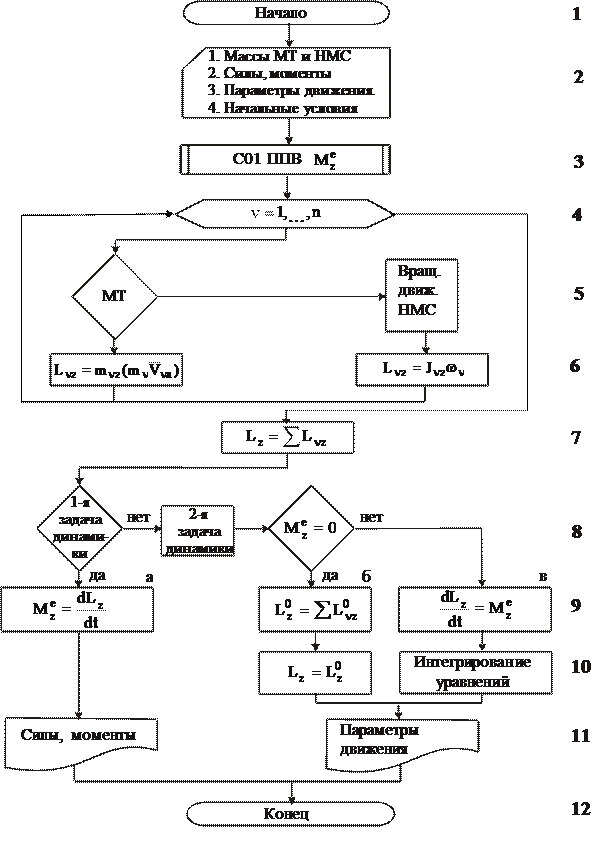
Комментарии

К.2.Рассматриваемый объект принимается за МС и указывается система координат (ось вращения), относительно которой исследуется движение. Выделяются и нумеруются МТ и НМС, входящие в МС.

На чертеже изображается силовая схема, т.е. изображаются все внешние силы и моменты, действующие на МС, в том числе внешние пассивные силы – силы реакций связи и реактивные моменты на основании принципа освобождаемости от связей (аксиома 5 статики). Определяются начальные условия.

К.6.Кинетический момент МС определяется для текущего или заданного момента времени. В выражение для момента количества движения МТ относительно оси входит ее абсолютная скорость, поэтому для отыскания 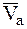может быть использована схема алгоритма К07 СДТ (Ч.1 Кинематика). Момент количества движения МТ относительно оси находится по тем же правилам, что и момент силы относительно оси (схема алгоритма С04 ППВ Ч.2 Статика), причем часто более удобно определять отдельно моменты количества переносного и относительного движений. Все скорости (угловые НМС и линейные МТ) выражаются либо через ту, которая задана, либо через ту, которую необходимо определить (может быть использована схема алгоритма К03 ВДТ Ч.1 Кинематика). Типовые формулы моментов инерции НМС приведены в таблице 2. Если ось вращения не проходит через центр масс, то применяется теорема Штейнера–Гюйгенса (формула (3.22)).

К.7.Суммирование моментов количеств движения МТ и НМС происходит с учетом их знаков.

К.10в.При интегрировании используется либо метод разделения переменных, либо теория линейных дифференциальных уравнений первого и второго порядков. Постоянные интегрирования находятся с помощью начальных условий.

Примечание

Теорема об изменении кинетического момента СМТ может быть использована при решении задач в тех случаях, когда НМС совершает вращательное движение относительно неподвижной оси, а МТ – любое движение.

Теорема об изменении кинетического момента СМТ также может быть использована при решении задач для НМС с одной закрепленной точкой (сферическое движение). В этом случае в уровнях 3 и 7 схемы алгоритма решения задач Д47 КМС главный момент внешних сил и кинетический момент определяются относительно трех осей.

Таблица 2