Вопрос 2. Электронная теория дисперсии.

Взаимодействие оптического излучения с веществом определяется взаимодействием электромагнитного поля световой волны с системой заряженных частиц, входящих в состав атомов и молекул вещества. Из электромагнитной теории Максвелла следует, что показатель преломления вещества определяется выражением:

,

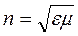где ε и μ – соответственно диэлектрическая и магнитная проницаемости среды. Для всех оптически прозрачных веществ μ ≈ 1, поэтому

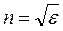, (11.1)

т.е. зависимость n = f(λ) определяется зависимостью диэлектрической проницаемости от частоты переменного электрического поля световой волны. Но в соответствии с теорией Максвелла величина 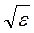является постоянной, а полученные из этого выражения значения n не согласуются с экспериментальными данными.

Для объяснения дисперсии света была предложена электронная теория Лоренца,в которой дисперсия света рассматривается как результат взаимодействия электромагнитных волн с заряженными частицами вещества, совершающими вынужденные колебания в переменном электромагнитном поле световой волны.

Ознакомимся с этой теорией на примере однородного изотропного диэлектрика. Диэлектрическая проницаемость вещества равна

ε = 1 + χ = 1 + ,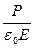

где χ – диэлектрическая восприимчивость среды, ε₀ – электрическая постоянная, Р – мгновенное значение поляризованности (наведенного дипольного момента единицы объема диэлектрика в поле волны с напряженностью электрического поля Е). Тогда

n² = 1 + 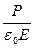, (11.2)

т.е. n зависит от Р. Для видимого света частота ω~10¹⁵ Гц столь велика, что существенны лишь вынужденные колебания внешних (наиболее слабо связанных) электронов атомов, молекул или ионов под действием электрической составляющей поля волны, а ориентационной поляризации молекул при такой частоте не будет. Эти электроны называются оптическими электронами.

Для простоты рассмотрим среду, в которой имеется лишь один сорт атомов и в каждом из них возможны колебания только одного оптического электрона. Наведенный дипольный момент электрона, совершающего вынужденные колебания, равен р = ех, где е – заряд электрона, х – смещение электрона из положения равновесия под действием электрического поля световой волны. Если n₀ – концентрация атомов в диэлектрике, тогда

Р = р n₀ = n₀ е х. (11.3)

Подставив (11.3) в (11.2) получим

n² = 1 + 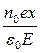, (11.4)

т.е. задача сводится к определению смещения х электрона под действием внешнего электрического поля Е = Е₀cos ωt.

Вынужденные колебания электрона, удерживаемого в атоме упругой силой, под действием внешней гармонической силы описываются уравнением:

d²x/dt² +ω₀² x = (F₀/m)cos ωt = (e/ m) E₀cos ωt, (11.5)

где F₀ = еE₀ – амплитудное значение силы, действующей на электрон со стороны поля волны, ω₀ = 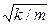– собственная частота колебаний электрона, m – масса электрона. Решив уравнение (11.5), найдем ε = n²в зависимости от констант атома (е, m, ω₀) ичастоты внешнего поля ω, т.е. решим задачу дисперсии.

Решением (11.5) является

х = А cos ωt, (11.6)

где

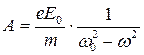. (11.7)

Подставим (11.6) и (11.7) в (11.4) и получим

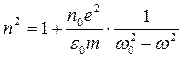. (11.8)

Если в атоме или молекуле вещества имеются различные заряды с массами m_i, способные совершать вынужденные колебания с собственными частотами ω_0i, то

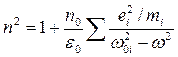. (11.9)

Из (11.8) и (11.9) видно, что показатель преломления вещества зависит от частоты ω внешнего электрического поля, и что в области частот от ω = 0 до ω ≤ ω₀ значение n² больше 1 и возрастает с увеличением частоты ω (нормальная дисперсия). Вблизи собственной частоты (ω = ω₀) значение n(ω) терпит разрыв, что соответствует поглощению света веществом; в области частот от ω ≥ ω₀ до ω = ∞ значение n² меньше 1 и возрастает от - ∞ до 1 (нормальная дисперсия). Перейдя от n² к n, получим зависимость n = n(ω), представленную на рис.11.1. Если учесть силы сопротивления при колебаниях электронов, то график зависимости n(ω) вблизи ω₀ дается линией АВ – область аномальной дисперсии. Куполообразная штриховая линия на рис.11.1 изображает зависимость коэффициента поглощения света веществом. Поглощение света в области аномальной дисперсии обусловлено интенсивным поглощением света на резонансной частоте.

Исследования аномальной дисперсии света в парах натрия были выполнены российским физиком Д.С. Рождественским. Он экспериментально показал справедливость формулы (11.9) и ввел дополнительную поправку, учитывающую квантовые свойства света и атомов вещества.