Уравнение сохранения энергии на межфазной поверхности

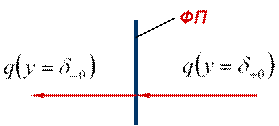
Межфазная поверхность

Здесь плотности тепловых потоков слева и справа от межфазной поверхности представляют собой перенос теплоты за счет теплопроводности и конвекции:

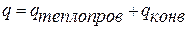
(13.13)

или

.

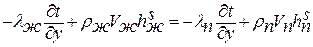(13.14)

Поскольку мы рассматриваем конденсацию сухого насыщенного пара, то переноса теплоты теплопроводностью в паровой области нет. Тогда:

.

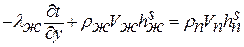(13.15)

Замечая, что разность энтальпий пара h_vs и жидкости h_ls на линии насыщения есть скрытая теплота конденсации r, r = h_vs – h_ls, и учитывая равенство потоков массы (уравнение неразрывности), получим:

,

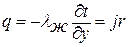(13.16)

или

.

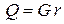(13.17)

Таким образом, первый важный для формулировки модели конденсации вывод будет следующим: теплота фазового превращения отводится от поверхности раздела фаз в пленку конденсата посредством теплопроводности (молекулярной).

Здесь j, кг/(м²с) – локальная плотность поперечного потока массы, или скорость конденсации, q, Вт/м² – локальная плотность теплового потока. Величины G, кг/(с),и Q, Вт, а j и q есть плотности потоков, отнесенные к единице поверхности стенки.

Уравнения движения для ламинарной гравитационной пленки если положить равным нулю трение на поверхности раздела фаз τ_S:

.

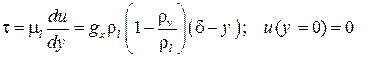(13.18)

Условие отсутствия динамического взаимодействия с паром τ_S = 0

.

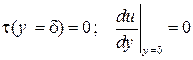(13.19)

учтено при записи уравнении движения. Действительно, при подстановке y = δ получается нулевое трение и нулевой градиент скорости на поверхности пленки.

Решением уравнения движения будет соотношение для профиля скорости

.

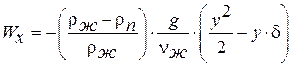(13.20)

Проверка показывает, что выполняются граничные условия на поверхности стенки (условие прилипания) и на межфазной поверхности трение равно нулю.

Профиль скорости и коэффициента теплоотдачи в пленке конденсата

Среднее значение скорости по толщине пленки конденсата равно:

.

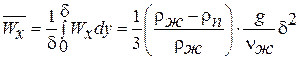(13.21)

Запишем уравнение теплового баланса в виде:

.

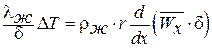(13.22)

Подставляя полученные соотношения для средней скорости получим выражение для определения толщины пленки:

.

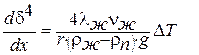(13.23)

Откуда с учетом δ(х=0)=0:

.

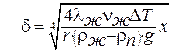(13.24)

И локальный коэффициент теплоотдачи при конденсации на вертикальной пластине (трубе) будет равен:

.

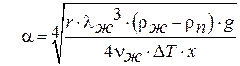(13.25)

Экспериментальные исследования подтверждают полученные расчетные зависимости.

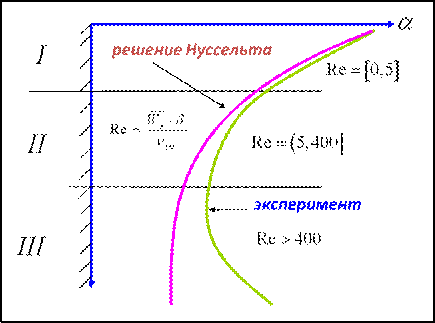
Сопоставление решения Нуссельта с экспериментом

Однако рекомендуется поправка на неучтенный в теории эффект волновых возмущений на поверхности раздела фаз. П.Л.Капица, занимавшийся этим вопросом в связи с течениями пленок жидкого гелия, оценил поправку примерно в 20% в сторону увеличения коэффициента теплоотдачи. Физический эффект состоит в том, что во впадинах волн, там где толщина пленки уменьшается, выигрыш от увеличения скорости конденсации получается больше, чем проигрыш на выступах волн. Полезно представить себе здесь характер зависимости α(δ) которая является нелинейной.

По рекомендациям Д.А.Лабунцова, мы будем учитывать волновую поправку как множитель к теоретическим формулам:

.

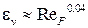(13.26)

Ламинарное течение с гладкой поверхностью пленки наблюдается при Re_F < 5. В интервале 5 < Re_F < 400 ламинарное течение сопровождается волнообразованием. Когда число Рейнольдса превосходит критическое значение, равное примерно 400, наблюдается переход к турбулентному режиму.