Физико – математическая постановка

Особенности гидродинамики и теплопереноса в жидкой фазе при пленочной конденсации обобщаются в форме модели тонкой пленки конденсата, согласно которой:

· Имеет место равномерное, без ускорений течение в пленке ( течение под действием уравновешивающих друг друга актуальных сил, таких как гравитация и вязкое трение)

· Давление постоянно по сечению пленки; оно будет таким же, как в паровом объеме, если пренебречь эффектом лапласовского давления, связанного с кривизной поверхности раздела

· Течение в пленке считается параллельным стенке; поперечные (нормальные к стенке) составляющие скорости принимаются равными нулю

· Продольная теплопроводность в пленке пренебрежимо мала; точно так же малы нормальные вязкие напряжения в поперечном сечении пленки

· Поперечный перенос теплоты и импульса определяется молекулярной теплопроводностью, молекулярной вязкостью.

· Для криволинейных стенок обычно принимают, что толщина пленки мала по сравнению с радиусом кривизны твердой поверхности.

Уравнение неразрывности на межфазовой поверхности (ФП). Количество сконденсировавшегося пара равно количеству образовавшегося конденсата:

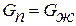
(13.4)

или

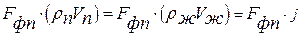
(13.5)

Здесь j-поток массы через границу раздела фаз.

Уравнение тепловой энергии:

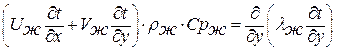
(13.6)

Нуссельт принял условие, что теплота транзитом передается к стенке, т.е.

.

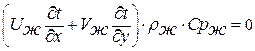(13.7)

Тогда уравнение тепловой энергии пленки конденсата принимает вид:

.

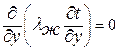(13.8)

Граничные условия на стенке и межфазной поверхности записываются как:

.

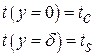(13.9)

Из решения уравнения энергии следует что градиент температуры постоянен по толщине пленки. Поэтому распределение температуры будет линейным, как для классической задачи о теплопроводности плоской стенки с постоянным коэффициентом теплопроводности l.

Решением уравнения энергии для пленки конденсата будет соотношение:

.

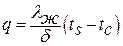(13.10)

Записывая соотношение для теплоотдачи при конденсации

,

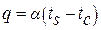(13.11)

и сопоставляя с предыдущим решением получаем:

.

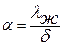(13.12)