Основное расчетное уравнение простого трубопровода (характеристика трубопровода).

Одной из основных задач расчета простого трубопровода является определение мощности, необходимой для транспортировки заданного расхода жидкости или газа от источника к потребителю, т.е. на определенное расстояние.

Рис.4.1. Схема простого трубопровода

Мощность, необходимая для транспортировки жидкостей и газов по трубопроводам, определяется по формуле:

, (43)

где Q – объемный расход жидкости (м³/с);

Δp – потребная разность давлений – перепад давлений, необходимый для транспортировки жидкости от источника к потребителю (Н/м²).

Часто выражение (43) записывают в виде:

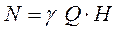, (44)

где 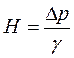– потребный напор; γ = ρg – удельный вес жидкости.

Потребная разность давлений Δp при установившемся движении жидкости складывается из:

-разности давлений источника и потребителя (р₂ – р₁);

-перепада давлений, обусловленного разностью уровней источника и потребителя [γ(z₂ –z₁)];

-потерь давления на трение по длине трубопровода Δp_l ,

-потерь давления на местных сопротивлениях Δp_м:

Δp=(р₂ – р₁)+ γ(z₂ –z₁)+ Δp_l+ Δp_м. (45)

Потери давления по длине трубопровода определяются по формуле Дарси:

,

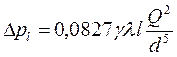где λ - коэффициент гидравлического трения, в общем случае является функцией числа Рейнольдса (Re) и относительной шероховатости (D/d),

Величина коэффициента λ определяется по графику ВТИ или по формулам для соответствующего режима течения.

В реальных трубопроводах обычно реализуется развитый турбулентный режим течения жидкости, отвечающий квадратичной зоне сопротивления, когда l = f(D/d) и не зависит от числа Re. Такой режим течения называется режимом развитой шероховатости. В этих случаях потери давления на трение по длине трубопровода можно определять по формуле:

,

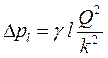где – модуль расхода трубы, k = f(d, Δ).

Значения k можно найти в справочниках для всего ассортимента труб, выпускаемых промышленностью.

Потери давления на местных сопротивлениях определяются по формуле:

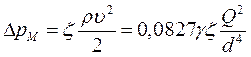, (46)

где ζ – коэффициент местного сопротивления.

Величина коэффициента местного сопротивления ζ зависит от вида местного сопротивления, его геометрических размеров, условий входа жидкости в него и от режима течения жидкости (т.е. от числа Рейнольдса Re).

Выражение (44) в совокупности с выражениями (45) и (46) иногда называют основным расчетным уравнением простого трубопровода.

Сумма (р₂ – р₁)+ γ(z₂ –z₁) = Δp_СТ – является величиной постоянной (не зависит от расхода Q) и называется статической разностью давлений, а соответствующий напор:

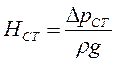(47)

называется статическим напором.

Сумма (Δp_l + Δp_м) является переменной составляющей потребной разности давлений (зависит от расхода Q) :

Δp_l+ Δp_м = F(Q).

Аналогично, сумма соответствующих потерь напора:

h_l +h_м = f(Q),

где ; .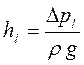

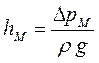Таким образом выражение (44) можно представить в виде суммы:

Δp = Δp_СТ + F(Q).

Соответствующее выражение для потребного напора будет иметь вид:

Н = Н_СТ+ f(Q).

Графическая зависимость потребного напора Н от расхода Q:

[ Н(Q)] (или Δp(Q)) называется графиком потребного напора (рис.4.2):

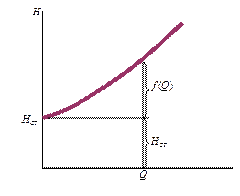
Рис.4.2. График потребного напора.

Графическая зависимость суммарных потерь напора в трубопроводе от расхода f(Q)=h_l+ h_м (или аналогичная зависимость для потерь давления в трубопроводе F(Q)=Δp_l + Δp_м) называется характеристикой трубопровода (рис.4.3).

Рис.4.3. Характеристика трубопровода.