Все законы физики имеют одинаковый вид во всех инерциальных системах отсчета.

Другими словами: все инерциальные системы физически эквивалентны друг другу и понятия абсолютного движения и абсолютного покоя лишены смысла.

Этот фундаментальный закон выражает тот опытный факт, что два любых опыта, поставленных одинаковым образом в двух разных инерциальных системах, дают одни и те же результаты, т.е. являются объективным отражением природы.

Поскольку физические законы обычно формулируются как количественные соотношения между различными физическими величинами и записываются в виде математических уравнений, принцип относительности утверждает неизменность (инвариантность) уравнений относительно перехода из одной инерциальной системы координат в другую.

Очевидно, что в физике должны существовать величины как относительные, так и абсолютные.

Рассмотрим последнее утверждение на примере преобразования координат Галилея. Пусть имеются две прямоугольных системы координат (x,y,z,t) и (x`,y`,z`,t`), причем система (x`,y`,z`,t`) движется с постоянной скоростью V вдоль оси х системы (x,y,z,t), как на рис 1.31.

z

t z` · M t`

V

x x`

O O`

y y`

Рисунок 1.31. К выводу преобразований координат Галилея

Определим координаты точки М в движущейся и неподвижной системах координат.

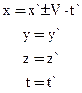
Этот набор уравнений учитывает возможность движения подвижной системы как в положительном, так и в отрицательном направлении оси х, а также тот факт, что в классической механике время во всех системах движется одинаково – длительность секунды везде одинакова.

Продифференцируем этот набор уравнений по t.

.

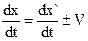По определению, 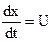– скорость движения точки М относительно системы координат (x,y,z,t), а 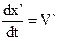– скорость движения т.М относительно системы координат (x`,y`,z`,t`).

Таким образом,

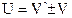, то есть скорость поступательного движения точки (тела) есть величина относительная.

Продифференцируем последнее соотношение еще раз:

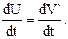
Поскольку по определению 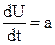– ускорению т.М в неподвижной системе координат, и 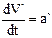– ускорению т.М в подвижной системе координат и а = а`, то, очевидно, следует считать, что ускорение является величиной абсолютной.

Поскольку в классической механике масса тела – также величина абсолютная, то абсолютной является и величина силы:

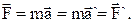
Понятно, что и уравнения движения, обязанного этим силам, будет одинаковым в любых инерциальных системах координат.

Не трудно показать, что абсолютной величиной в классической физике является также длина отрезка, пространственного промежутка. Пусть в неподвижной системе координат находится прямой абсолютно твердый стержень с координатами концов (x₁,y₁,z₁) и (x₂,y₂,z₂). Его длина L равна

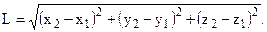
Используя преобразования координат Галилея, можно показать, что

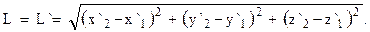
(x`<sub>1</sub>,y`₁,z`<sub>1</sub> и x`₂,y`<sub>2</sub>,z`₂, - координаты концов стержня в подвижной системе координат, все члены, содержащие произведение vt, сократятся).

Естественный скептический вопрос: каковы же границы применимости преобразований Галилея возник перед человечеством к конце ХIX – начале ХХ веков. Возник он в связи с поиском Абсолютной системы отсчета (на существовании которой сам Ньютон, кстати, не настаивал). Он возник в связи с изучением парадоксальных свойств эфира – гипотетической абсолютно упругой среды, в которой свет распространяется без затухания, как в абсолютно твердой среде. В то же самое время обычные макротела движутся в этой среде, «не замечая» ее бесконечной твердости…

Сомнения в бесконечной применимости преобразований Галилея, по крайней мере, в части закона сложения скоростей, возникли при анализе результатов опытов Майкельсона-Морли по определению скорости «эфирного ветра» из сравнения скорости света, излученного источником, движущимся вдоль направления перемещения Земли на орбите и скорости света вдоль направления, перпендикулярного касательной к орбите. Измерения производились на чрезвычайно точном приборе - интерферометре Майкельсона (рисунок 1.32). Земля остроумно была выбрана в качестве объекта, движущегося с линейной скоростью 30 км/сек, практически до сих пор недостижимой современной техникой для массивных объектов.

Схему опыта предложил Максвелл , автор электромагнитной теории света. Он должен был позволить обнаружить движение Земли относительно эфира, если бы свет распространялся в эфире, а эфир покоился бы в гелиоцентрической системе координат.

Опыт Майкельсона, впервые поставленный в 1881 году, и давший отрицательный ответ, поставлен был фундаментально: плита толщиной до 0,5 м, на которой смонтированы зеркала, была изготовлена из гранита, слабо расширяющегося с нагреванием, и плавала в ртути для бездеформационного поворота. Первичная точность опыта позволяла обнаружить «эфирный ветер» при скорости 10 км/с. Позднее он многократно повторялся, точность была повышена до возможности обнаружения ветра со скоростью 30 м/с. Но ответ был стабильно нулевым.

Рисунок 1.32 а) Общий вид интерферометра Майкельсона. б) Принципиальная схема опыта Майкельсона. Луч света от источника 1 расщепляется в полупрозрачной пластинке Р на два луча 1 и 2,идущие вдоль и перпендикулярно направлению движения Земли по орбите. Скорость движения Земли по орбите отмечена стрелкой и буквой V. Лучи света 1 и 2 отражаются соответственно от зеркал S₁ и S₂ и вновь возвращаются к пластинке Р. После отражения и преломления в направлении 3 идут два луча. В этом направлении и наблюдается интерференционная картина. Решающий шаг эксперимента состоит в повороте всей установки на 90°; луч 1 идет теперь по направлению движения Земли, а луч 2 - нормально движению. Если бы свет распространялся по неподвижному эфиру, оптическая разность хода лучей 1 и 2 стала бы иной и интерференционная картина, наблюдаемая в направлении 3, изменилась бы (произошло бы смещение интерференционных полос). Однако никакого смещения полос опыт не обнаружил.

Преобразования Галилея не подтвердились при наблюдении движений с большими скоростями. Например, не оказалось нарушений в ритме периодического движения двойных звезд, между тем как направление скорости их движения меняется на прямом и обратных путях обращения. Скорость света, таким образом, оказалась не зависящей от движения источника.

Со времени проведения опытов Майкельсоном и Морли в 1881 году и до 1905 года – до разработки основ СТО – делались многочисленные попытки выработать гипотезы, в которых результаты ключевого опыта нашли бы объяснение. И при этом все пытались сохранить эфир, видоизменяя лишь его свойства.

Наиболее известны любопытные попытки ирландского физика Джорджа Фитцджеральда и голландского физика Хендрика Лоренца. Первый предложил идею сокращения длины тела в направлении движения, тем большего, чем выше скорость движения. Лоренц предположил возможность локального течения времени («местное время») в подвижной системе, по законам, отличающимся от закономерностей в неподвижной системе. Лоренц предложил модифицировать преобразования координат Галилея.

Преобразование координат Лоренца:

x` = k · (x - V · t); x = k · (x` + V · t`);

y` = y; y = y`;

z` = z; z = z`;

t` = k · (t - x ·V / c<sub>2</sub>); t = k · (t` + x` · V / c²);

По виду лоренцевские преобразования заметно отличаются от галилеевских лишь в части описания времени. Коэффициент k определяется из соотношения

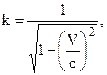
где V – скорость движения подвижной системы вдоль оси Х неподвижной, с – скорость света в вакууме с=3×10⁸ м/с. Остальные обозначения - прежние. Заметьте, что переход из одной системы в другую осуществляется переменой знака с одновременным переносом штрихов справа налево или наоборот.

Сам Лоренц рассматривал свой набор уравнений как подгонку уравнений под результаты эксперимента Майкельсона-Морли, Лоренц умер в 1928 году, так и не примирившись с мыслью о ненужности эфира.

Очень значительные усилия в направлении решения этого вопроса были сделаны французом Анри Пуанкаре (по его предложению в 1904 году вышеприведенный набор уравнений был назван преобразованиями координат Лоренца).