Промежуток времени между событиями

Пусть в системе K' в одной и той же точке с координатой x' происходят в моменты времени t'₁ и t'₂ два каких-то события. Это могут быть, например, рождение элементарной частицы и ее последующий распад. В системе K' эти события разделены промежутком времени

Dt' = t'₂ ‑ t'₁.

Найдем промежуток времени Dt между событиями в системе K, относительно которой система K' движется со скоростью V. Для этого определим в системе K моменты времени t₁ и t₂, соответствующие моментам t'₁ и t'₂ и образуем их разность:

Dt = t₂ — t₁.

Подстановка в нее значений координаты и моментов времени приводит к выражениям

.

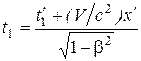
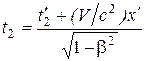Отсюда

.

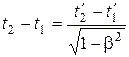Если события происходят с одной и той же частицей, покоящейся в системе K', то Dt' = t'₂ —t'₁ представляет собой промежуток времени, измеренный по часам, неподвижным относительно частицы и движущимся вместе с ней относительно системы K со скоростью v, равной V (напомним, что буквой V мы обозначаем только относительную скорость систем; скорости частиц и часов мы будем обозначать буквой v). Время, отсчитанное по часам, движущимся вместе с телом, называется собственным временем этого тела и обычно обозначается буквой τ. Следовательно, Dt' = Dτ. Величина Dt == t₂ — t₁ представляет собой промежуток времени между теми же событиями, измеренный по часам системы K, относительно которой частица (вместе со своими часами) движется со скоростью v. С учетом сказанного

.

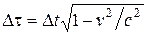Из полученной формулы следует, что собственное время меньше времени, отсчитанного по часам, движущимся относительно тела (очевидно, что часы, неподвижные в системе K, движутся относительно частицы со скоростью —v). В какой бы системе отсчета не рассматривалось движение частицы, промежуток собственного времени измеряется по часам системы, в которой частица покоится. Отсюда следует, что промежуток собственного времени является инвариантом, т. е. величиной, имеющей одно и то же значение во всех инерциальных системах отсчета. С точки зрения наблюдателя, «живущего» в системе K, Dt есть промежуток времени между событиями, измеренный по неподвижным часам, а Dτ— промежуток времени, измеренный по часам, движущимся со скоростью v. Поскольку Dτ < Dt, можно сказать, что движущиеся часы идут медленнее, чем покоящиеся часы. Подтверждением этого служит следующее явление. В составе космического излучения имеются рождающиеся на высоте 20—30 км нестабильные частицы, называемые мюонами. Они распадаются на электрон (или позитрон) и два нейтрино. Собственное время жизни мюонов (т. е. время жизни, измеренное в системе, в которой они неподвижны) составляет в среднем примерно 2 мкс. Казалось бы, что даже двигаясь со скоростью, очень мало отличающейся от c, они могут пройти лишь путь, равный 3·10⁸·2·10^‑6 м. Однако, как показывают измерения, они успевают в значительном количестве достигнуть земной поверхности. Это объясняется тем, что мюоны движутся со скоростью, близкой к c. Поэтому их время жизни, отсчитанное по часам, неподвижным относительно Земли, оказывается значительно большим, чем собственное время жизни этих частиц. Следовательно, не удивительно, что экспериментатор наблюдает пробег мюонов, значительно превышающий 600 м. Для наблюдателя, движущегося вместе с мюонами, расстояние до поверхности Земли сокращается до 600 м, поэтому мюоны успевают пролететь это расстояние за 2 мкс.

Интервал

В обычном пространстве расстояние Dl между двумя точками с координатами x_i, у₁, z₁ и x₂, у₂, z₂. определяется выражением

,

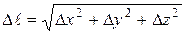где Dx = x₂ ‑ x₁ и т. д. Это расстояние не зависит от выбора системы координат, т. е. является инвариантом. При переходе к другой координатной системе изменяются, вообще говоря, величины Dx, Dy и Dz, однако эти изменения таковы, что расстояние Dl остается одним и тем же.

Казалось бы, что расстояние (или, как принято говорить, интервал) между двумя мировыми точками в четырехмерном пространстве-времени должно определяться аналогичным выражением

,

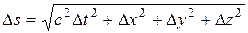где Dt = t₂ ‑ t₁ и т. д. Однако это выражение непригодно в качестве интервала, поскольку оно не является инвариантом — при переходе к другой инерциальной системе отсчета числовое значение этого выражения изменяется. Инвариантным, как мы покажем, является выражение

,

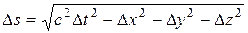которое называют интервалом между событиями. Величина Ds является аналогом расстояния Dl между точками в обычном пространстве.

Причина того, что интервал определяется не выражением

,

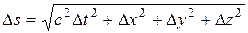а выражением

………… ,

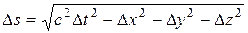заключается в том, что, как говорят, метрика пространства-времени отличается от метрики обычного трехмерного пространства. В обычном пространстве справедлива евклидова геометрия, вследствие чего его называют евклидовым. Качественное различие между временем и пространством приводит к тому, что в выражение для интервала квадрат временной координаты и квадраты пространственных координат входят с разными знаками. Пространство, в котором расстояние между точками определяется выражением вида 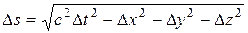, называется псевдоевклидовым. Его можно написать в виде

,

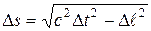где Dl — расстояние между точками обычного пространства, в которых произошли данные события.

Допустим, что рассматриваются события, происходящие с одной и той же частицей. Тогда отношение Dl/Dt дает скорость частицы v. Поэтому, вынеся из-под корня cDt, получим, что

.

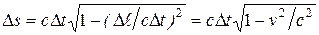Мы получили выражение 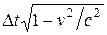. Оно равно Dτ — промежутку собственного времени частицы между событиями. Таким образом, мы приходим к соотношению

Ds = c·Dτ.

Поскольку c — константа, а Dτ—инвариант, интервал Ds также оказывается инвариантом.