Релятивистское выражение для энергии
В релятивистской механике справедливым остается выражение
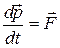 .
.
Это означает, что  . Откуда видно, что сила не является инвариантной величиной. Кроме того, сила F и ускорение a не коллениарны.
. Откуда видно, что сила не является инвариантной величиной. Кроме того, сила F и ускорение a не коллениарны.
Легко получить выражение для кинетической энергии.
Пусть тело (частица) ускоряется при прямолинейном движении вдоль 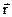 постоянной силой F, работа которой будет трансформироваться в прирост кинетической энергии
постоянной силой F, работа которой будет трансформироваться в прирост кинетической энергии
 ,
,
причем мы не можем, как раньше, выносить m за знак дифференцирования как константу, потому что при v~c m¹const. Поскольку 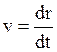 , поменяем порядок дифференцирования по координате
, поменяем порядок дифференцирования по координате

Рассмотрим теперь подробнее релятивистское выражение для массы
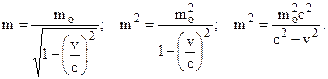
Упростим последнее выражение:
m2c2 – m2v2 = mo2c2Þ m2c2 = mo2c2 + m2v2
и продифференцируем с учетом условия mo = const и c=const:
2c2m×dm = 2mv2dm + 2m2v×dv½: 2m.
Получаем
с2dm = v2dm + mv×dv.
Сравним правые части уравнений и приравняем левые части этих уравнений
dT = c2dm.
Проинтегрируем последнее равенство при учете, что при v=0 T=0, a m=mo
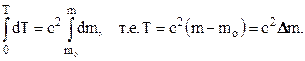
Итак,
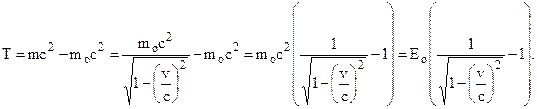
Понятно, что Ео =moc2 – энергия покоя тела, а mc2 – полная энергия тела, а их разность Т и есть кинетическая энергия, энергия, обусловленная движением тела.
Следствия:
1) Выражение Ео =moc2, впервые полученное Эйнштейном, характеризует полный запас энергии, содержащийся в любом теле.
2) Из релятивистского соотношения кинетической энергии привычное 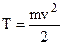 может быть легко получено в предельном случае vÞ0. Действительно, при v<<c
может быть легко получено в предельном случае vÞ0. Действительно, при v<<c
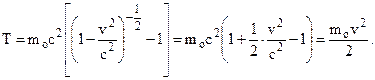
При релятивистском движении иначе выглядит и уравнение связи импульса частицы с её кинетической энергией
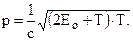
Энергия и импульс в релятивистской механике не сохраняются. Инвариантом является выражение:
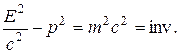
Дата добавления: 2017-10-04; просмотров: 1250;











