Обобщение данных единичных опытов

Вид критериальных зависимостей остается одинаковым для всех геометрических подобных систем, поскольку сохраняют силу исходные дифференциальные уравнения и условия однозначности. Количественная связь между критериями подобия на основании теории размерности обычно представляется в виде степенных зависимостей, позволяющих описать практически любую экспериментальную зависимость, тем более что критериальные уравнения представляют собой функции, изменяющиеся монотонно. Поэтому они легко могут быть аппроксимированы по отдельным интервалам приближенными степенными уравнениями.

В настоящее время эта форма критериальных уравнений получила очень большое распространение.

Прежде чем обрабатывать опытные данные в числах подобия, нужно знать, от каких чисел зависит определяемое значение. Для этого составляют систему дифференциальных уравнений, описывающих экспериментально изучаемый процесс, и формируют условия однозначности. Затем математическое описание процесса приводится к безразмерному виду.

Предположим, было получено, что 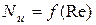, т.е. опыты проводились с теплоносителем, критерий Прандтля которого является постоянной величиной, не зависящей от температуры.

В этом случае зависимость между числами подобия обычно представляют в виде степенных функций, т.е.

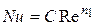, (5.4)

где 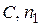– постоянные безразмерные числа.

Постоянные 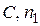подлежат определению. Для этого вычисляют значения критериев 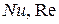по найденным из опыта величинам коэффициента теплоотдачи и скорости движения жидкости. По этим значениям критериев строят график. В нем по оси ординат откладывают 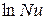, а по оси абсцисс – 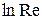. В указанных координатах опытные данные описываются прямолинейной зависимостью, что следует из уравнения (5.4).

.

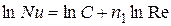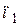Последнее уравнение является уравнением прямой линии. Показатель степени представляет собой тангенс угла наклона прямой к оси абсцисс.

Следовательно, значение 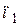можно определить с помощью графического представления опытных данных в координатах 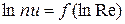(рис.5.1).

Показатель степени

.

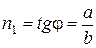Постоянная 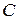определяется из уравнения

.

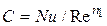Проверкой применимости степенной зависимости является тот факт, что в логарифмических координатах все полученные точки укладываются на прямую. Если же опытные точки располагаются по кривой, то эту кривую заменяют ломанной. Для отдельных участков такой кривой значения 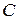и 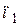различны.

В случае, если искомая величина Nu является функцией двух аргументов, например 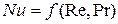, т.е. 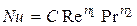, на графике получается семейство прямых, второй аргумент берется в качестве параметра (рис.5.2).

Тогда по одной из прямых определяют показатель при числе 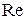, а затем опытные данные представляют на графике в виде зависимости 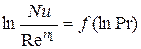. Из последнего графика определяют показатель степени 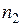при критерии 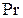, а значение коэффициента 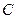определяют из уравнения

.

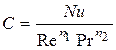Аналогичным путем можно установить и более сложные зависимости.

Критерии подобия, а, следовательно, и уравнения связи между ними обычно получают в предположении о независимости физических параметров жидкости от температуры.

Однако в процессе теплообмена, протекающих при высоких тепловых потоках и при больших скоростях, физические параметры жидкости нельзя считать постоянными. В этих случаях может иметь место резкое изменение температуры по сечению потока. При исследовании капельных жидкостей теплоотдача оказывается различной в условиях нагревания и охлаждения. Явная зависимость теплоотдачи от направления теплового потока объясняется тем, что при нагревании и охлаждении жидкости закономерности изменения скорости и температуры в пограничном слое различны вследствие различного характера изменения ее физических свойств. Поэтому процессы теплообмена, одни из которых протекают в условиях нагревания, а другие – в условиях охлаждения, строго говоря, не являются подобными процессами.

Физические параметры капельных жидкостей изменяются с температурой существенно, особенно вязкость. Для учета неизотермичности в этом случае применяются параметрические критерии в виде отношения значений вязкости или в виде отношений критериев Прандтля соответственно при температурах потока вдали (в центре) и у стенки трубы

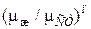и .

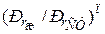Критерии подобия имеют нулевую размерность. Определяющая температура, по которой выбираются физические параметры, может быть принята произвольно. Она принимается, в основном, исходя из соображения удобства расчетов. В качестве определяющей температуры принимают такую температуру, которая в технических расчетах бывает задана или легко вычислена.

В качестве линейного характерного размера можно принимать расстояния 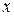или 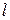и другие величины.

Для каналов круглого сечения в качестве определяющего размера обычно принимается внутренний диаметр. Для каналов некруглого сечения широко применяется эквивалентный диаметр

,

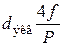где 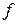и 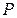– соответственно площадь и периметр поперечного сечения канала.

Для кольцевых каналов рекомендуется еще вводить множитель, характеризующий соотношение между диаметрами, так как для случая ламинарного стабилизированного течения вязких жидкостей пользоваться эквивалентным диаметром для расчета теплоотдачи нельзя.