Метод электрогидродинамических аналогий (метод ЭГДА)
Метод ЭГДА успешно применяют для изучения стационарных физических процессов, которые описываются уравнениями эллиптического вида.
В этом случае метод ЭГДА применяется в горном деле и гидротехнике для решения задач фильтрации жидкости; в электротехнике – для решения задач электропередачи; в строительной механике – при решении задач теории упругости; в теплотехнике – для решения задач теплообмена, а также для решения задач диффузии газа и жидкости, распространения магнитных, электрических и взрывных волн и др.
В ряде случаев, используя метод суперпозиций, метод ЭГДА может быть применен и для решения нестационарных физических процессов, которые описываются уравнениями параболического типа, например, задачи замораживания горных пород и фильтрации жидкости и газа в пористых средах, физические процессы которых протекают весьма медленно во времени. В этом случае изучение процесса в заданный период времени разбивается на сравнительно короткие промежутки времени, в течение которого физический процесс может рассматриваться как стационарный с соответствующим заданием граничных условий.
Метод ЭГДА основан на математической аналогии между некоторыми физическими процессами: например, между стационарным движением электрического тока в проводящей среде или стационарным распространением тепла в твердых телах, диффузией газа и жидкости и т.д.
Рассмотрим аналогию указанных выше процессов на примере аналогии
между стационарным движением электрического тока в проводящей среде и стационарным движением жидкости в пористых средах. Для упрощения процесса рассмотрим для плоскости (двухмерная задача). В этом случае процессы описываются следующими уравнениями
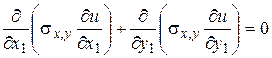 ; (6.55)
; (6.55)
уравнение неразрывности
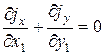 . (6.56)
. (6.56)
Для фильтрующих пород:
уравнение движения
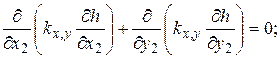 (6.57)
(6.57)
уравнение неразрывности
 (6.58)
(6.58)
где  – электрический потенциал;
– электрический потенциал;
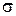 – электропроводность материала;
– электропроводность материала;
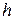 – пьезометрический напор;
– пьезометрический напор;
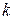 – коэффициент фильтрации;
– коэффициент фильтрации;
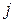 – компоненты плотности тока;
– компоненты плотности тока;
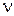 – компоненты скорости потока;
– компоненты скорости потока;
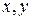 – координаты поверхности.
– координаты поверхности.
Если среды однородные, то коэффициенты электропроводности и фильтрации будут постоянными. В этом случае вместо уравнений (6.55), (6.57) получим уравнения Лапласа:
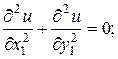
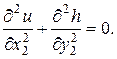
Исходя из этих уравнений, устанавливают аналогию между процессами и отдельными параметрами (табл.6.2).
Таблица 6.2
| Электрическое поле тока | Поле фильтрации жидкости | Магнитное поле | Поле температур |
Закон Ома:
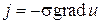 ; ;
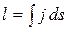 ,
где ,
где 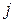 – плотность тока; – плотность тока; 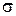 – электропроводность; – электропроводность;
 – электрический потенциал; – электрический потенциал; 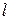 – сила тока. – сила тока.
| Закон Дарси:
 ; ;
 ,
где ,
где 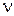 – скорость фильтрации; – скорость фильтрации;
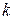 – коэффициент фильтрации; – коэффициент фильтрации; 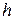 – пьезометрический напор; – пьезометрический напор; 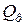 – фильтрационный расход. – фильтрационный расход.
| Закон магнитной индукции:
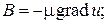
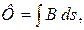 где
где 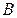 – магнитная индукция; – магнитная индукция;
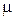 –магнитная проницаемость; –магнитная проницаемость;  – магнитный потенциал; – магнитный потенциал; 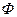 – магнитный поток. – магнитный поток.
| Закон Фурье:

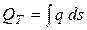 ,
где ,
где 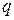 – тепловой поток; – тепловой поток; 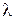 – коэффициент теплопроводности; – коэффициент теплопроводности;
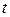 – температура; – температура; 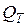 – тепловой поток. – тепловой поток.
|
Таким образом, исследование вопросов фильтрации в натуре сводят к изучению соответствующих (аналогичных) электрических процессов и параметров на электрических моделях, и результаты этих исследований распространяют на процессы фильтрации.
При осушении месторождений полезных ископаемых в результате работы водопонизительных скважин образуется депрессионная поверхность, на основании которой ведутся все гидрогеологические расчеты (дебит скважин и установки в целом, расположение скважин в плане, приток воды в горные выработки, закладка фильтров и т.д.). Для получения на электрической модели процессов аналогичных процессам фильтрации жидкости в натуре, необходимо выполнить ряд условий, вытекающих из общей теории подобия.
1. Электрическая модель должна представлять изучаемую область фильтрации жидкости в натуре в некотором масштабе без всякого искажения, т.е. должно быть соблюдено геометрическое подобие.
2. Коэффициент электропроводности модели должен быть прямо пропорционален в сходственных точках коэффициенту фильтрации жидкости, т.е. между моделью и натурой должно быть соблюдено физическое подобие
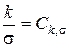 . (6.59)
. (6.59)
3. Также должны быть подобны граничные условия модели и натуры, т.е. должно быть соблюдено динамическое подобие
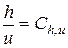 . (6.60)
. (6.60)
Подставив значения параметров фильтрации из выражений (6.59) и (6.60) в выражение (6.57), после преобразований получают
 (6.61)
(6.61)
Следовательно, уравнения (6.55) и (6.61) будут аналогичными в том случае, если произведение коэффициентов в квадратных скобках будет постоянно:
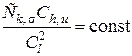 . (6.62)
. (6.62)
Для однородной среды при 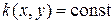 и
и 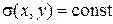 условия физического подобия выполняются автоматически, т.е. имеет место автомодельность. Поэтому при моделировании физических процессов необходимо соблюдать только геометрическое и динамическое подобие.
условия физического подобия выполняются автоматически, т.е. имеет место автомодельность. Поэтому при моделировании физических процессов необходимо соблюдать только геометрическое и динамическое подобие.
Исследование процесса осушения водоносных пород в конечном счете сводится к определению напоров воды на различных участках изучаемого пространства. Следовательно, на электрической модели необходимо построить поле потенциала, которое было бы аналогичным депрессионной поверхности воды в натуре. Пересчет электрического потенциала на напоры воды производится на основании граничных условий моделирования, которые могут быть записаны следующим образом:
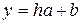 , (6.63)
, (6.63)
где 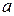 и
и 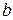 – постоянные коэффициенты.
– постоянные коэффициенты.
При этом:
при 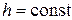 должно быть
должно быть 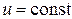 ;
;
при 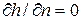 должно быть
должно быть 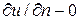 .
.
В этом случае будем иметь:
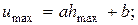 (6.64)
(6.64)
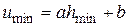 . (6.65)
. (6.65)
Значения максимальных и минимальных напоров воды обычно известны. Максимальный напор воды 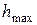 имеет место на границе области питания и определяется гидрогеологическими разведочными скважинами. Контур питания определяется гидрогеологическими расчетами или непосредственными наблюдениями в скважинах при опытных откачках. Минимальный напор воды
имеет место на границе области питания и определяется гидрогеологическими разведочными скважинами. Контур питания определяется гидрогеологическими расчетами или непосредственными наблюдениями в скважинах при опытных откачках. Минимальный напор воды 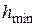 задают из условий работы водопонизительных скважин. На электрической модели в соответствии с заданием максимального и минимального напоров воды задают максимальные и минимальные напряжения
задают из условий работы водопонизительных скважин. На электрической модели в соответствии с заданием максимального и минимального напоров воды задают максимальные и минимальные напряжения 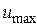 и
и 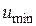 . Обычно на модели эквипотенциальные поля строятся в относительных величинах. При этом
. Обычно на модели эквипотенциальные поля строятся в относительных величинах. При этом 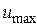 берется за 1, а
берется за 1, а 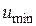 0. Подставив значения
0. Подставив значения 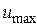 = 1 и
= 1 и 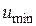 = 0 в выражения (6.64) и (6.65), получим:
= 0 в выражения (6.64) и (6.65), получим:
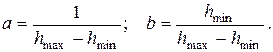 (6.66)
(6.66)
Следовательно, значение потенциала в любой точке поля будет определяться формулой
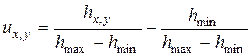 . (6.67)
. (6.67)
Зная значения 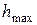 и
и 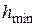 и значение потенциала
и значение потенциала  на модели (определяется прибором), получим для напорной фильтрации значение напора
на модели (определяется прибором), получим для напорной фильтрации значение напора 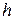 в любой точке изучаемой области натуры:
в любой точке изучаемой области натуры:
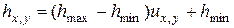 . (6.68)
. (6.68)
В случае безнапорной фильтрации пересчет от потенциалов к напорам производится по формуле
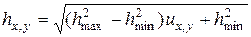 . (6.69)
. (6.69)
При напорно-безнапорной фильтрации каждая из вышеприведенных формул (6.68) и (6.69) применяется в соответствующей области. Граница между ними определяется из условия
 , (6.70)
, (6.70)
где 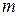 – мощность водоносного пласта.
– мощность водоносного пласта.
Принцип действия установки ЭГДА основан на использовании для производства экспериментов мостового (компенсационного) метода измерений электрического потенциала в поле модели. Принципиальная электрическая схема установки ЭГДА (рис.6.4) состоит из блока питания и блока измерения.
 В блок питания входят: понизительный трансформатор 1, выпрямитель 2 и измерительные приборы – вольтметр 3 и миллиамперметр 4. В блок измерений входит: градуированный потенциометр 5, нуль-индикатор (гальванометр) 6 и поисковая игла 7.
В блок питания входят: понизительный трансформатор 1, выпрямитель 2 и измерительные приборы – вольтметр 3 и миллиамперметр 4. В блок измерений входит: градуированный потенциометр 5, нуль-индикатор (гальванометр) 6 и поисковая игла 7.
Если поисковой иглой подключиться к модели в какой-то точке 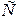 , то будут иметь место отмеченные на схеме токи
, то будут иметь место отмеченные на схеме токи 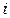 и потенциал
и потенциал  . Если же градуированное сопротивление потенциометра 5 отрегулировать так, чтобы потенциал
. Если же градуированное сопротивление потенциометра 5 отрегулировать так, чтобы потенциал 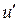 в точке
в точке 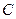 был равен потенциалу
был равен потенциалу  в точке
в точке 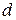 , то мост будет уравновешен, в чем убеждаются по отсутствию отклонения стрелки гальванометра: так как
, то мост будет уравновешен, в чем убеждаются по отсутствию отклонения стрелки гальванометра: так как 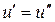 , то
, то 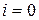 .
.
При уравновешенном мосте в силу разности потенциалов в точках а и б ток пойдет частично через модель, а частично через градуированный потенциометр и тогда:
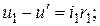
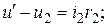
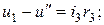
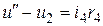 .
.
Если 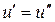 , то
, то 
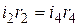 .
.
Разделив их, получим
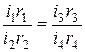 , (6.71)
, (6.71)
а так как 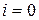 (в сети гальванометра), то
(в сети гальванометра), то 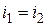 и
и 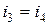 .
.
Отсюда получаем уравнение равновесия моста
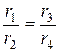 или
или 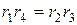 (6.72)
(6.72)
Принимая сопротивление модели за усредненно-линейное, получаем значение потенциала 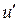 на всей линии
на всей линии 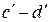 . Это и есть линия равного потенциала
. Это и есть линия равного потенциала 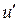 . Но так как
. Но так как 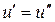 , то по шкале градуированного потенциометра в момент равновесия мостовой схемы получим значение потенциала
, то по шкале градуированного потенциометра в момент равновесия мостовой схемы получим значение потенциала 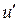 в той точке, где установлена поисковая игла.
в той точке, где установлена поисковая игла.
Из теории моста следует, что
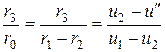 . (6.73)
. (6.73)
Отсюда ясно, что результаты измерений потенциалов на моделях не зависят от величины напряжения, приложенного на шинах модели, т.е. при изменении напряжения  (при колебании напряжения в питательной сети) одновременно и пропорционально изменяется падение напряжения
(при колебании напряжения в питательной сети) одновременно и пропорционально изменяется падение напряжения 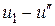 . Поэтому разность потенциалов
. Поэтому разность потенциалов  может быть условно принята равной единице, а различные эквипотенциальные линии на модели будут лежать в пределах от нуля до единицы.
может быть условно принята равной единице, а различные эквипотенциальные линии на модели будут лежать в пределах от нуля до единицы.
Зная значения отдельных эквипотенциалей [или в пересчете по формулам (352), (353) напоров] и кратчайшие расстояния между ними, можно определить величину градиентов, а также плотность тока или скорости фильтрации.
Таким образом, метод ЭГДА дает возможность заменить исследования фильтрационного потока в натуре исследованием электрического поля на модели и результаты исследования перенести в натуру.
Дата добавления: 2017-10-04; просмотров: 4378;











