Метод тепло-гидравлических аналогий

При разработке месторождений полезных ископаемых часто приходится встречаться с тепловыми задачами, например, теплообмен при замораживании горных пород, при разработке месторождений полезных ископаемых на больших глубинах или в условиях вечномерзлых пород и т.д. В большинстве случаев задачи теплообмена представляют собой весьма сложные физические процессы, которые в общем случае описываются уравнениями параболического типа с первой производной во времени. Для решения указанных задач успешно применяют метод гидравлических аналогий, разработанный проф. В.С. Лукьяновым. Метод гидравлических аналогий применяют также для решения фильтрационных, диффузных и других задач. Аналогия между термическим и гидравлическим процессами легко устанавливается при сравнении основных уравнений рассматриваемых процессов. Однако, придерживаясь основных положений моделирования, принятых в настоящей книге, установим аналогию между процессом распространения тепла в пластине и движением вязкой жидкости по капиллярам.

Как известно, расход жидкости за участком стабилизации может быть определен по формуле

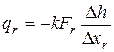, (6.74)

где 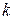– гидравлическая проводимость капилляра;

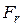– площадь сечения капилляра;

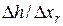– падение напора на участке капилляра .

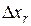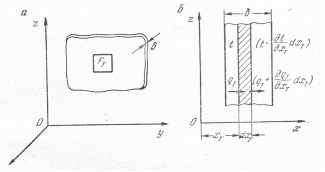
Рассмотрим теперь распространение тепла в пластине (рис.6.5),

Рис.6.5. Схема к расчету теплообмена в пластине: а-общая схема; б-теплообмен через элементарный слой.

толщина которой исчезающее мала по сравнению с ее высотой и шириной. Если подвод или отвод тепла осуществляется равномерно к каждой из внешних поверхностей пластины, то температура будет изменяться только вдоль оси 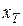. При этом количество тепла, проходящего через площадку 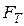в направлении оси x_T

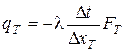, (6.75)

где 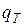– количество тепла, проходящего через площадку ;

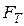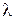– коэффициент теплопроводности пластины;

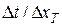– падение температуры на участке пластины толщиной .

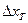Нетрудно видеть, что уравнения (6.74) и (6.75) имеют одинаковую структуру. При этом 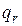является аналогом 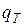; 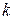является аналогом 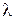; 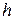является аналогом 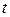; 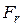является аналогом 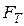; 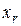является аналогом .

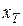Таким образом, законы, управляющие распространением тепла в пластине и ламинарным течением вязкой жидкости, выражаются аналогичными уравнениями. Это дает основание полагать, что дифференциальные уравнения, полученные из этих законов, будут аналогичными.

Выделим в пластине (см. рис.6.5, а), в которой происходит нестационарный режим распространение тепла, элементарный слой толщиной 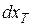(см. рис.6.5, б).

При этом физические параметры пластины ( 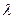– теплопроводность; 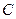– теплоемкость; 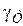– удельный в материала пластины) будем рассматривать как постоянные величины.стьость; параметры пластины (ежим распространение тепла, элементарный слой толщиной

Количество тепла, входящего за время 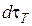в левую поверхность элементарного слоя, определится как

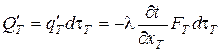. (6.76)

Но так как тепловой поток распространяется только в сторону понижения температуры, а температурный градиент, представляющий вектор, имеет положительное направление в сторону возрастания температуры, то в формуле температурный градиент берется с обратным знаком.

Количество тепла, выходящего за то же время через правую поверхность элементарного слоя,

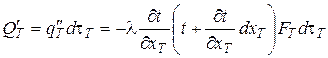. (6.77)

Разность между количеством тепла, которое вошло в рассматриваемый элементарный слой за время 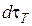и вышло из него за тот же промежуток времени

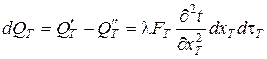. (6.78)

Очевидно, эта разность тепла пошла на изменение теплосодержания элементарного слоя за то же время, т.е.

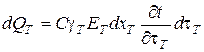, (6.79)

где 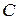– удельная теплоемкость материала пластины;

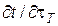– температурный градиент.

Согласно закону сохранения энергии при отсутствии источников тепла в рассматриваемом элементарном слое правые части формул (6.78) и (6.79) должны быть равны и тогда будем иметь

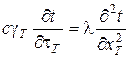или 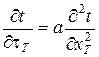, (6.80)

где 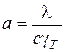– коэффициент температуропроводности.

Перейдем к выводу дифференциального уравнения для гидравлической системы. С этой целью представим схему (рис.6.6).

Рис.6.6. Схема к расчету гидравлической модели: а – общая схема; б – схема одного капилляра; 1 – пьезометры; 2 – капилляры; 3 – внешний капилляр; 4 – сосуд постоянного уровня.