Техническим состоянием оборудования в эксплуатации

2.9.1. Модель технологической долговечности [1]

Техническое состояние оборудования в процессе эксплуатации изменяется. В результате медленно протекающих процессов старения машина из работоспособного состояния переходит в неработоспособное.Граница между этими состояниями зависит от требований производства, для одних требований производ­ства машина будет считаться работоспособной, а для других — не­работоспособной. Работоспособное состояние восстанавливается в результате мероприятий технического обслуживания (ТО) и ремонта (Р).

Точность машины в эксплуатации меняется в пределах допуска на обработку от a₀ до a_max (рис. 2.8). Кривая а(t) получается путем соединения всех то­чек, характеризующих точность машины в начале каждого межналадочного периода, как показано в интервале Δt₁. Трансформация а(t) происходит с переменной скоростью, увеличивающейся со временем.

Рис. 2.8. Графическая интерпретация математической модели технологической долговечности

a(t) - точность работы в начале межналадочного периода (разрегулировочная кривая);

a_р (t) – точность отрегулированной машины (кривая износа);

a₀ - начальная точность машины;

a_max – максимально допустимая неточность машины;

∆t – время работы между регулировками;

Т - время работы между ремонтами.

В момент времени Т дальнейшая эксплуатация машины нецелесообразна так как время между регулировками сильно сокращается. В этот момент производится ремонт машины, но достичь начального уровня точности a₀ не удается, так как ремонтируются не все детали и узлы машины.

Приблизительно можно считать

a(t) - a_р (t) = K ( t_i – t_i-1 ); (2.15)

При t_i - t_n

a_max - a_р (t_n) = K ∆t_n (2.16)

Исследованиями доказано, что скорость изменения потери точности вследствие износа (a_р (t) – a₀ )ʹ пропорциональна точности (в пределах межрегулировочного периода)

(a_р (t) – a₀ )ʹ = a_р (t)ʹ = λ a(t) , (2.17)

где λ – коэффициент пропорциональности.

Решая это дифференциальное уравнение, получим выражение, из которого определяется длительность межрегулировочных промежутков

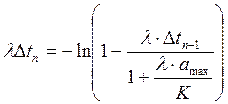. (2.18)

Период работы до ремонта

. (2.19)

Коэффициенты K и λ рассчитываются по формулам

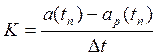, (2.20)

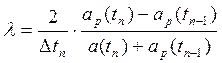. (2.21)

Параметры a(t_i), a_р (t_i), a_р (t_i-1) определяются из экспериментальных замеров при эксплуатации оборудования.

2.9.2. Модель безотказности [1]

Модель безотказности показывает характер изменения вероятности безотказной работы P(t) во времени (рис. 2.9).

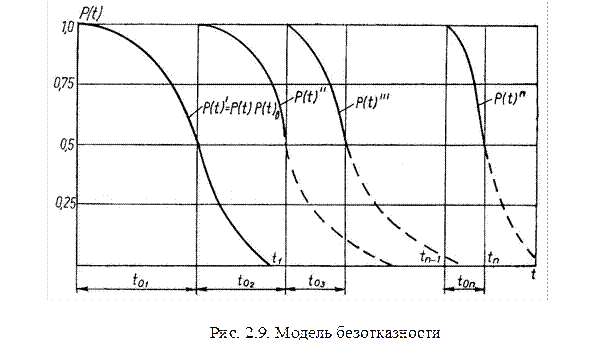Предельный уровень безотказности, после которого работа машины нецелесообразна, для механических систем деревообрабатывающего оборудования принимают равным P(t)_пред =0,5…0,8. На рис. 2.9 предельный уровень безотказности принят P(t)_пред =0,5.

В момент времени t_oi машина должна подвергаться операциям восстанавливающим её качество до максимально возможного P(t)→1. Затем цикл вновь повторяется, но закон изменения P(t)ʹʹ может отличаться от P(t)ʹ так как не все узлы ремонтируются одновременно.

В общем виде согласно формуле (2.10)

P(t) = P_пост(t) P_вн(t),

где P_пост(t) – вероятность безотказной работы при постепенных отказах изменяется в соответствии с нормированной функцией Лапласа;

P_вн(t) – вероятность безотказной работы при внезапных отказахизменяется в соответствии с экспоненциальным законом.

2.9.3. Модель технического состояния оборудования [1]

Модель технического состояния машины состоит из моделей технологической долговечности и безотказности. Графиче­ская ее интерпретация приведена на рис. 2.10. Таким образом, техническое состояние оборудования характеризуется технологической точностью и безотказностью элементов.

Начальная точность машины может быть определена по ре­зультатам приемосдаточных испытаний на заводе-изготовителе оборудования или взята по аналогии с уже имеющимися ма­шинами. Предельное значение точности определяется по регла­ментированному для данной машины и вида обработки квалитету. Затем определенный период времени Δt_i машина работает под на­грузкой в реальной эксплуатации или в испытаниях, после чего в момент t_i измеряется её точность a(t_i). Машина под­вергается регулировке, и вновь измеряется точность. Получен­ные данные дают возможность определить значения скоростей разрегулировки К и износа λ и построить модель технологи­ческой долговечности. Эти же данные и параметры надежности составных частей машины позволяют построить модели безотказ­ности.

В ряде случаев возможно совпадение отказов по точности и отказов элементов. Это происходит оттого, что, как правило, выход из строя формообразующих элементов машины вызы­вает снижение точности.

Безотказность может быть ниже 0,5 при запасе технологической долговечности вследствие отказов элементов.