Определение надежности машины

Для расчета показателей надежности необходимо иметь информацию об отказах машины и её элементов или о скорости и характере процессов старения. Информация о скорости процесса старения более ценная, так как позволяет осуществлять прогноз поведения машины, в то время как све­дения об отказах дают лишь констатацию того или иного уровня надежности.

На практике используются обычно три основных источника информации о надежности машины: эксплуатационные испыта­ния; стендовые испытания; аналитический (расчетный) метод.

Основные источники получения информации о надежности – эксплуатационные и стендовые испытания. Главная цель испытаний – определение уровня надежности машины и выявление причин, снижающих этот уровень. В процессе испытаний опре­деляют фактические сроки службы основных деталей машины и выявляют наименее долговечные. Устанавливают при­чины отказов машины и их физическую сущность. Исследуют динамику износа основных деталей и узлов, рассчитывают показатели надежности, и закономерности их изменения во времени.

Аналитический (расчетный) метод позволяет судить о зна­чениях показателей надежности машины на стадии ее проекти­рования; до минимума сокращает время, необходимое для определения показателей надежности; позволяет выявить зависи­мости между показателями надежности и параметрами, харак­теризующими конструкцию, технологию изготовления, условия и режимы эксплуатации. Однако расчетный метод в настоящее время мало применяется вследствие недостаточного развития теоретической базы.

Один из методов расчета [2] рассматривает машину как сложную систему, состоящую из отдельных узлов, деталей, аг­регатов, систем управления и т. д.

Надежность любой сложной системы обусловлена надеж­ностью элементов, из которых она состоит, их количеством и характером их взаимосвязей. Такими элементами служат: в автоматиче­ской линии – отдельные рабочие машины, станки, агрегаты; в рабо­чей машине – функциональные узлы (механизмы резания, подачи, базирования, суппорты, шпиндели), приспособления и т. д.; в узле – детали, сопряжения, поверхности. Каждый элемент системы можно рассматривать как совокупность более простых элементов.

Элементы могут быть соединены в систему по одной из сле­дующих схем: последовательной, параллельной, последователь­но-параллельной. Последовательной называется схема, при которой выход из строя любого из элементов вызывает пре­кращение функционирования всей системы. В параллельной схеме работа отдельных элементов не зависит друг от друга. При выходе из строя одного элемента система продолжает функционировать. Как разновидность параллельной схемы имеются схемы с резервированием, в которых вместо потерявшего работоспособность элемента включается в работу новый элемент — автоматически или вручную. В последователь­но-параллельной схеме элементы соединены последовательно, но менее надежные дублируются.

Подавляющее большинство систем деревообрабатывающего оборудования состоит из последовательно соединенных элемен­тов. Так, если в приводе машины выйдет из строя любая шестерня, подшипник, муфта, рычаг управления, электро­двигатель или другая деталь, то весь привод перестанет функ­ционировать.

Вероятность безотказной работы такой системы равна произведению вероятностей безотказной работы элементов:

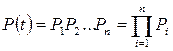. (2.7)

Если причина выхода из строя деталей машины или узла связана только с внезапными отказами, то в соответствии с формулой (2.6)

; ; …

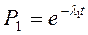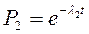Подставив это в формулу (2.7), получим

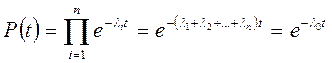, (2.8)

где

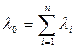. (2.9)

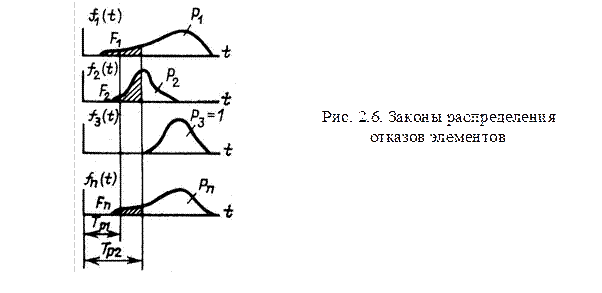
Для постепенных отказов для каждого элемента характерен свой закон распределения отказов элементов, например, как показано на рис. 2.6.

Большинство деревообрабатывающего оборудования рабо­тает в условиях, когда подверженные изнашиванию детали и узлы могут выйти из строя также и из-за внезапных отказов. Вероятность безотказной работы в этом случае можно опреде­лить с помощью теоремы умножения вероятностей

P(t) = P_пост(t) P_вн(t), (2.10)

где P_пост(t) – вероятность безотказной работы при постепенных отказах;

P_вн(t) – вероятность безотказной работы при внезапных отказах.

Рассмотрим кривые вероятности безотказности работы при совместном дейст­вии постепенных и внезапных отказов (рис. 2.7).

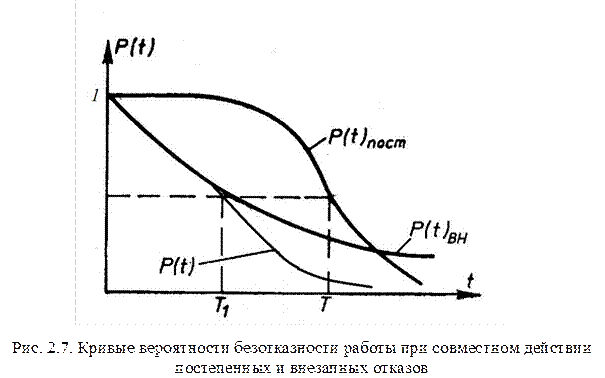
На графиках видно, что до ка­кой-то наработки Т₁ функция надежности P(t) подчиняется экспо­ненциальному закону, т. е. в этот период преобладают вне­запные отказы так как износа почти нет. По мере накопления износа роль постепенных отказов возрастает и кри­вая надежности резко убывает, приходя в большее согласие с законом нормального распределения.

Иногда для того, чтобы с большей точностью передать ха­рактер падения надежности при сложном взаимодействии по­степенных и внезапных отказов, прибегают к закону распределения отказов Вейбулла [1].

Для повышения надёжности сложных систем применяют резервирование. При резервировании дублируют элементы с низкой надёжностью. При выходе из строя одного из элементов, дублёр выполняет его функции. Различают нагруженное резервирование, когда дублирующие элементы постоянно присоединены и работают параллельно, и ненагруженное (холодное) резервирование, когда дублирующие элементы включаются в работу только после выхода из строя основных элементов (рис. 2.8).

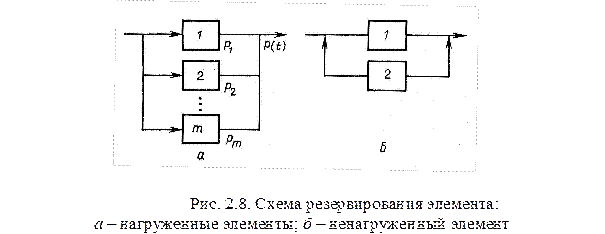
При нагруженном резервировании, когда резервные элементы постоянно находятся в работе, вероятность безотказной работы рассчитывается следующим образом. Пусть F₁; F₂; …F_m – вероятность появления отказа каждого из элементов за время t=T. Тогда в нагруженном резервировании вероятность совместного появления отказов всех элементов за время t

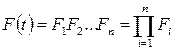. (2.11)

И вероятность безотказной работы системы с параллельным резервированием элементов будет

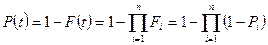. (2.12)

Средняя наработка на отказ T_i является величиной обратной интенсивности отказов λ_i

.

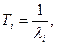
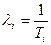При ненагруженном (холодном) резервировании резервные элементы находятся в отключенном состоянии до момента выхода из строя основного элемента и вероятность безотказной работы равна

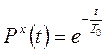. (2.13)

Средняя наработка на отказ при холодном дублировании определяется по формуле [1]

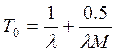, (2.14)

где M - среднее время восстановления работоспособности (время ремонта), ч.