Дифференциальное уравнение конвективноготеплообмена
При конвективном теплообмене тепло распространяется одновременно теплопроводностью и конвекцией. Уравнение переноса тепла теплопроводностью 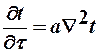 , где
, где 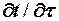 - это локальное изменение температуры неподвижного элемента среды. При конвективном переносе тепла среда движется и в данном случае изменение температуры элемента среды запишется:
- это локальное изменение температуры неподвижного элемента среды. При конвективном переносе тепла среда движется и в данном случае изменение температуры элемента среды запишется:
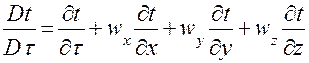 . Т.о. дифференциальное уравнение конвективного переноса тепла имеет вид и называется уравнением Фурье- Кирхгофа:
. Т.о. дифференциальное уравнение конвективного переноса тепла имеет вид и называется уравнением Фурье- Кирхгофа:
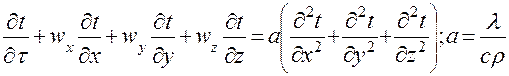 ( 13 )
( 13 )
Уравнение ( 11 )выражает распределение температур в движущейся жидкости. В данном уравнении t является функцией различных переменных, в том числе скорости и плотности жидкости. Поэтому уравнение (11) должно рассматриваться совместно с уравнениями движения Эйлера и уравнением неразрывности. Однако полученную систему уравнений аналитически решить невозможно. Поэтому для практического использования уравнение подобно преобразовывают с учетом условий однозначности, т.е. представляют в виде функции от критериев подобия.
Тепловое подобие
У поверхности твердого тела, находящегося в движущейся жидкости всегда имеется пограничный слой толщиной d через который тепло передается теплопроводностью в направлении перпендикулярном движению потока. Рассмотрим подобие граничных условий. По закону Фурье количество тепла проходящее в пограничном слое толщиной d через площадь dF за время dt составляет 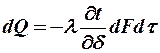 .
.
Количество тепла, проходящее от стенки в ядро потока, определяется по з.Ньютона
dQ=adFdtDt, где Dt=tст-tж.
При стационарном режиме теплообмена количество тепла, проходящее через пограничный слой и ядро потока равны:
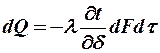 =adFdt (tст-tж)
=adFdt (tст-tж) 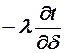 =a (tст-tж).
=a (tст-tж).
Для подобного преобразования разделим правую часть на левую и отбросим знаки математических операторов; dзаменим определяющим размером 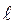 (эль). Получим безразмерный критерий Nu = a
(эль). Получим безразмерный критерий Nu = a 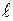 /l -критерий Нуссельта. Критерий Нуссельта характеризует интенсивность теплообмена на границе раздела фаз.Nu - является мерой соотношения толщины пограничного слоя d и определяющего геометрического размера (если это труба, то ее диаметр).
/l -критерий Нуссельта. Критерий Нуссельта характеризует интенсивность теплообмена на границе раздела фаз.Nu - является мерой соотношения толщины пограничного слоя d и определяющего геометрического размера (если это труба, то ее диаметр).
Рассмотрим условия подобия в потоке. Возьмем уравнение Фурье-Кирхгофа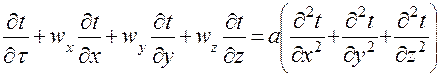
ß ß ß
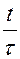 (1)
(1) 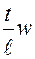 (2)
(2) 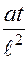 (3)
(3)
Разделим (1) на (3) получим безразмерный комплекс 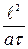 . Чтобы не оперировать с дробными числами, берут обратную величину
. Чтобы не оперировать с дробными числами, берут обратную величину 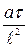 =F0 - критерий Фурье - характеризует связь между скоростью изменения температурного поля, размерами и физическими характеристиками среды в нестационарных тепловых процессах.
=F0 - критерий Фурье - характеризует связь между скоростью изменения температурного поля, размерами и физическими характеристиками среды в нестационарных тепловых процессах.
Разделим (2) на (3) –получим 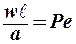 – критерий Пекле- характеризует отношение количеств тепла, распространяемых в потоке жидкости конвекцией и теплопроводностью. Критерий Pe может быть представлен как произведение Re*Pr = Pe;
– критерий Пекле- характеризует отношение количеств тепла, распространяемых в потоке жидкости конвекцией и теплопроводностью. Критерий Pe может быть представлен как произведение Re*Pr = Pe; 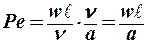 .
.
Критерий Прандтля Pr – характеризует поле теплофизических величин потока жидкости и находится только по теплофизическим параметрам жидкости 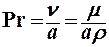 . В тех случаях, когда теплообмен осуществляется в результате естественной конвекции, процесс характеризуется критерием Архимеда Ar = (gl3/n2)*(r-r0)/r, где r,r0 –плотности холодной и нагретой жидкости. Поэтому комплекс (r-r0)/r заменяют на bDt. Получают Критерий Грасгофа
. В тех случаях, когда теплообмен осуществляется в результате естественной конвекции, процесс характеризуется критерием Архимеда Ar = (gl3/n2)*(r-r0)/r, где r,r0 –плотности холодной и нагретой жидкости. Поэтому комплекс (r-r0)/r заменяют на bDt. Получают Критерий Грасгофа 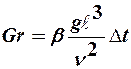 , ( где b - коэффициент объемного расширения жидкости,
, ( где b - коэффициент объемного расширения жидкости, 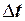 - разность температур стенки и жидкости).
- разность температур стенки и жидкости). 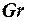 – характеризует гидродинамический режим потока жидкости в условиях естественной конвекции, происходящей под влиянием разности плотностей нагретой и холодной жидкости.
– характеризует гидродинамический режим потока жидкости в условиях естественной конвекции, происходящей под влиянием разности плотностей нагретой и холодной жидкости.
Дата добавления: 2017-10-04; просмотров: 1234;











