Движущая сила тепловых процессов
Движущей силой тепловых процессов является разность температур сред, при наличии которой тепло передается от среды с большей tо к среде с меньшей tо.
При теплопередаче от одного теплоносителя к другому разность между температурами теплоносителей не сохраняет постоянного значения вдоль поверхности теплообмена. Потому в тепловых расчетах, где применяется основное уравнение теплопередачи к конечной поверхности теплообмена, необходимо пользоваться средней разностью температур или температурным напором.
При выводе формулы для ∆tср. рассмотрим теплообменник, работающий прямотоком.Сделаем рисунок.
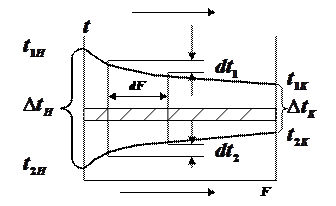

С одной стороны стенки с поверхностью F движется более нагретый теплоноситель с нач.tо-t1н, теплоемкостью с1 ( 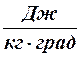 ), расходом G1 (кг/с).
), расходом G1 (кг/с).
С другой стороны – менее нагретый теплоноситель с нач. .tо-t2н, теплоемкостью с2, расходом G2.
Причем примем, что теплоемкости постоянны в течении всего процесса теплообмена. Теплообмен происходит через стенку, площадь поверхности которой F. Процесс теплопередачи установившийся.
Вследствие теплообмена, по мере течения теплоносителей вдоль стенки их температуры будут изменяться и, следовательно, и разность температур ∆t между теплоносителями.
Возьмем элемент поверхности dF. На элементе поверхности dF более нагретый теплоноситель охлаждается на dt1 град., а менее нагретый нагревается на dt2 град. Значит для элемента поверхности dF можно записать уравнение теплового баланса:
Введем водяные эквиваленты:
dQ = G1с1(-dt1) = G2с2dt2, G1с1 = W1, G2с2 = W2.
(Произведение расхода теплоносителя G на его теплоемкость называется водяным эквивалентом W. Численно W означает кол-во воды, которое по своей тепловой емкости эквивалентно количеству тепла, необходимого для нагревания теплоносителя на 1оС при заданном его расходе.).
dQ = W1(-dt1) = W2dt2
Знак “ - “ означает, что более нагретый теплоноситель охлаждается.
-dt1 = 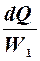 ; dt2 =
; dt2 = 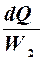 ;
;
Сложим: d(t1 – t2) = - dQ( 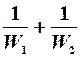 ), обозначим (
), обозначим ( 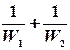 ) = m,
) = m,
d(t1 – t2) = 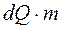 ;
;
d(∆t) = - 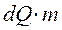 ; dQ = -
; dQ = - 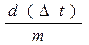 . (a)
. (a)
В соответствии с основным уравнением теплопередачи:
dQ = KdF∆t (б)
Приравниваем (а) и (б):
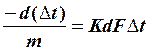
d(∆t) = - KdF∆t m . (в)
Разделим переменные и проинтегрируем выражение (в) в пределах изменения ∆t (от t1н-t2н = ∆tн до t1к-t2к = ∆tк) и dF (от 0 до F). При этом считаем, что K=Const.
Тогда:
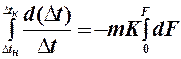 , где ∆tн и ∆tк – концевые движущие силы.
, где ∆tн и ∆tк – концевые движущие силы.
ℓn 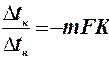 (г)
(г)
Запишем уравнение теплового баланса для всей поверхности F:
Q = W1(t1н – t1к) = W2(t2н – t2к);
W1 = 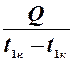 ; W2 =
; W2 = 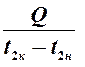 ;
;
m = 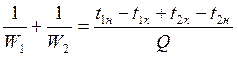
имея в виду ∆tн = t1н-t2н, ∆tк = t1к-t2к, получим
m = 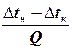 ; Подставим в (г)
; Подставим в (г)
ℓn 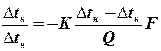 ; откуда
; откуда
Q = 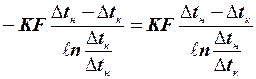 . (*)
. (*)
Сопоставим полученное выражение с основным уравнением теплопередачи. Видно, что ∆tср (средняя движущая сила или средний температурный напор) представляет собой среднелогарифмическую разность температур:
∆tср = 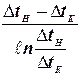 (**)
(**)
Уравнение (*) является уравнением теплопередачи при прямотоке теплоносителей. С помощью (*) по известным Q тепловой нагрузке и известным tн1,2 и tк1,2 теплоносителей можно определить величину поверхности теплообмена F.
Из уравнения (г) следует: ∆tк = ∆tн℮-mKF. Этоозначает, что при прямотоке температуры теплоносителей изменяются ассимптотически.
Уравнение (**) справедливо и для противотока, если в него подставить соответственно ∆tδ и ∆tм.
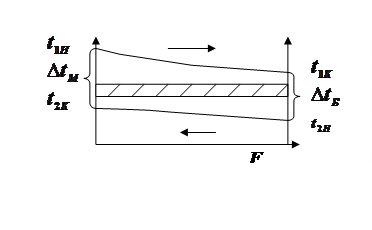
∆tδ = t1к – t2н ; ∆tм= t1н – t2к
Если 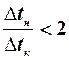 ; (
; ( 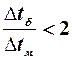 ), то ∆tСР с достаточной точностью можно определить как среднеарифметическую разность: ∆tср =
), то ∆tСР с достаточной точностью можно определить как среднеарифметическую разность: ∆tср = 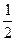 (∆tк +∆tн).
(∆tк +∆tн).
Дата добавления: 2017-10-04; просмотров: 1565;











