Условия и анализ последствий неадекватного поведения ЭС для информационной и информационно-управляющей системы (А3)

Ниже будем рассматривать сложные информационные и информационно-управляющие системы S, обладающие свойст-вом открытости [32, 50], то есть, такие системы, которые являют-ся инвариантными по отношению к программно-аппаратным реализациям, обеспечивающими переносимость прикладных про-грамм, взаимодействие и функциональное расширение систем [21, 24, 51-54].

Пусть система S состоит из {s} элементов, тогда простран-ство {U} – множество всех решений, возможных для класса от-крытых информационных систем с {s} - числом составляющих элементов, пространство {U*} – множество всех решений, воз-можных для класса открытых информационных систем с {s} - числом составляющих элементов с учетом воздействия внешней среды на систему (имеется в виду возможное возникновение но-вых решений при несанкционированном воздействии внешней среды), {R} – множество разрешенных решений, {Z} – множест-во запрещенных решений. Очевидно, что .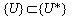
Утверждение 2.1. Пусть {S} – множество решений, опреде-ляемое задачами функционирования системы S. Тогда существу-ет хотя бы 1 элемент множества {S}, принадлежащий {Z}.
Доказательство будем проводить от противного. Пусть та-кой элемент не существует, тогда возможны две ситуации:

- {S}={U*}, что невозможно из-за ограниченности возмож-ностей реальных вычислительных систем, реализующих данную информационную систему,

- {S}={U}, то есть отсутствует влияние внешних случайных воздействий, что для реальных систем невозможно.

Следовательно, хотя бы один элемент множества {S} при-надлежит {Z}. Такой элемент (элементы) будет образовывать множество {SZ}, являющееся подмножеством как множества {S}, так и {Z}.

Выявление элементов множества (SZ} определяет задачи моделирования разрабатываемых информационных систем, либо тестирования уже существующих систем.

Утверждение 2.2. Невозможно выявление всего множества элементов {SZ} в результате моделирования, либо тестирования.
Чтобы смоделировать функционирование системы S, то есть определить множество {S}, необходимо смоделировать функцио-нирование системы с учетом влияния самого процесса моделиро-вания, то есть определить множество {S}+{SM1}, что, в свою очередь, требует определения множества {S}+{SM1}+{SM2}, и так далее до бесконечности, где множества {SMI} определяют возможность возникновения дополнительных решений из-за воз-действия процесса моделирования на систему на i-той итерации анализа.
Таким образом, Утв.2.2. можно сформулировать как невоз-можность на этапе разработки полного определения всех несанк-ционированных решений системы, поэтому возможна только по-становка задачи возможно более полного их выявления. При этом, без учета внешних и внутренних случайных воздействий можно определить весь перечень несанкционированных реше-ний, а с учетом таких воздействий – только некоторую часть.

Утверждение 2.3. Нельзя при моделировании ограничиться действием только значимых факторов, или, иначе, незначимый фактор в конкретный момент времени может привести к перехо-ду множества решений системы из {SR} в {SR'}, где

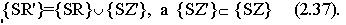
Сформулированные выше утверждения дают методологиче-скую основу для проведения анализа последствий неадекватное поведение ЭС для информационно-управляющих систем.

Основными особенностями такого анализа являются:
- отсутствие кратных ребер в графе G в силу отсутствия вза-имных, в том числе неэлектрических, влияний (помимо чисто информационного обмена) между ЭС;

- отсутствует обратное влияние между смежными ЭС.

Из перечисленных особенностей видно, что алгоритм А3 анализа последствий неадекватного поведения для информаци-онной и информационно-управляющей систем будет аналогичен алгоритму А0, только в качестве вершин графа будут выступать ЭС, в которых осуществляется преобразование и хранение ин-формации, а также информационный обмен.