Соосными поверхностями вращения называются поверхности, имеющие общую ось вращения.

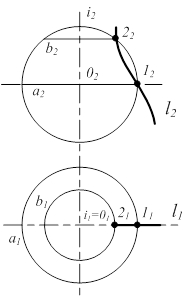
Соосные поверхности вращения всегда пересекаются по окружностям, плоскости которых перпендикулярны оси вращения. Этих окружностей столько, сколько существует точек пересечения очерковых линий поверхностей (рис. 6.17).

S1 ® поверхность вращения кривой l S2 ® сфера 0 Ì i ; 1 Î l Þ a Ì S1 2 Î l Þ b Ì S1 (a,b) = S1 Ç S2

Рисунок 6.17

Вспомогательные концентрические сферы применяются при следующих условиях:

1) обе поверхности являются поверхностями вращения;

2) оси вращения поверхностей пересекаются, они имеют общую плоскость симметрии.

i¹Ç i² = 0 , центр всех вспомогательных секущих сфер;

3) нельзя использовать способ применения вспомогательных секущих плоскостей, т.к. они не дают графически простых линий пересечения с заданными поверхностями.

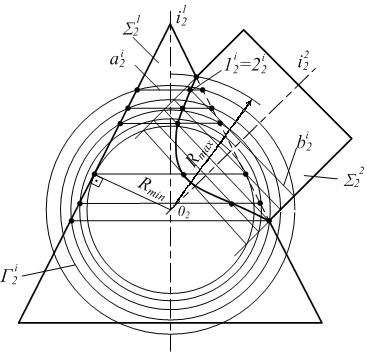
Задача(рис. 6.18).

Вводя вспомогательные сферы получим достаточное число искомых точек линии пересечения.

Радиус вспомогательных сфер изменяется равномерно в пределах:

R_min ≤ R ≥ R_max.

R_max - определяется расстоянием от центра 0 до наиболее удаленной точки линии пересечения очерков поверхностей.

R_min - определяется, как радиус сферы, касающейся одной поверхности (по окружности) и пересекающей другую.

Плоскости окружностей касания или пересечения перпендикулярны осям вращения поверхностей. В пересечении этих окружностей получаются точки, принадлежащие линии пересечения заданных поверхностей.

Горизонтальные проекции точек пересечения находятся по принадлежности их поверхности конуса.

S1 - коническая поверхность вращения, ось i1 S2 - цилиндр вращения, ось i2 i1Ç i2 = 0 S1 Ç S2 = m 1) G i - сфера с центром в т.0; 2) G i Ç S1 = аi G iÇ S2 = bi - окружности, вырожденные в отрезки 3) аi2 Ç bi2 = {1i2,2i2} Ì m - - точки линии пересечения поверхностей.

Рисунок 6.18

Горизонтальная проекция линии пересечения конуса и цилиндра строится по принадлежности точек линии пересечения поверхности конуса.

Вопросы для самоконтроля:

1) Укажите алгоритм решения задач на пересечение плоскостей, когда обе плоскости занимают общее положение.

2) Укажите алгоритм решения задач на пересечение прямой и плоскости, когда они занимают общее положение

3) Укажите алгоритм решения задач на пересечение поверхностей или поверхности и плоскости, когда они занимают общее положение.

4) Перечислите условия применения секущих концентрических сфер.