Жёсткий режим возбуждения
Если выбрать рабочую точку, так чтобы крутизна была меньше критической (см. рис. 7.2, точка B и 7.3, точка H), то генерация сама не возникнет. Более того, если, например, за счёт внешнего источника, вызвать колебания в контуре амплитуды меньшей UЗИ(G), то после выключения внешнего источника колебания затухнут, и колебаний в системе не будет. Как показано на рис. 7.3, будут две стационарные точки, в которых положительное сопротивление компенсируется вносимым отрицательным. Видно, что левая точка (G) будет неустойчивой. Действительно, при случайном увеличении амплитуды напряжения на конденсаторе увеличится и ток IСИ, а, следовательно, увеличится подкачиваемая в контур энергия (увеличится отрицательное сопротивление). Это приведёт к ещё большему увеличению амплитуды напряжения на конденсаторе и т.д.
Важно, что при включении генератора (при нулевой начальной амплитуде) автоколебания не разовьются. И только если начальная амплитуда вынужденных колебаний превысит амплитуду UЗИ(G), то в системе установятся устойчивые колебания амплитуды UЗИ(F). Наоборот, правая стационарная точка (F) будет устойчивой.
Такой режим называют жёстким режимом.

Рис. 7.3. Пример зависимости средней крутизны 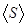 (UЗИ), для жёсткого режима возбуждения автоколебаний.
(UЗИ), для жёсткого режима возбуждения автоколебаний.
Весьма наглядным оказывается описание процессов в автогенераторе с помощью фазовой плоскости, по осям которой мы отложим напряжение 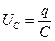 на конденсаторе и скорость изменения заряда, то есть нормированный ток
на конденсаторе и скорость изменения заряда, то есть нормированный ток 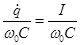 .
.
Как известно, колебания осциллятора без потерь на фазовой плоскости соответствуют движению точки по окружности или эллипсу, горизонтальная полуось которого равна амплитуде колебаний. Затухающие колебания в свободном осцилляторе описываются сходящейся спиралью. Тогда стационарные автоколебания в контуре автогенератора будут соответствовать устойчивому движению по часовой стрелке вдоль окружности, радиус которой равен амплитуде q0 стационарных колебаний. Причём, если первоначально амплитуда колебаний была больше или меньше стационарной, то со временем такие траектории будут все ближе приближаться к стационарной окружности. Эта окружность называется устойчивым предельным циклом. В случае мягкого режима предельный цикл один и он устойчивый, в случае жёсткого режима – предельных циклов два, один из которых неустойчивый, а другой – устойчивый. Сказанное иллюстрирует рис. 7.4.

МЯГКИЙ
РЕЖИМ
Дата добавления: 2017-10-04; просмотров: 1143;











