Условия возникновения автоколебаний

Как было показано в предыдущем разделе, коэффициент усиления усилителя с обратной связью определяется выражением:

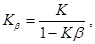
где K – коэффициент усиления усилителя без обратной связи, а β – коэффициент передачи цепочки обратной связи. Из этой формулы следует, что при Kβ → 1 величина K_β неограниченно увеличивается. Это соответствует условию самовозбуждения, при котором развиваются автоколебания. Устройства, в котором возникают автоколебания, называются автогенераторами.

Подчеркнём, что K = K(ω) = 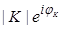и β = β(ω) = 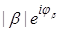– комплексные величины. Поэтому условие самовозбуждения соответствует двум условиям:

|K| |β| ≥ 1, (7.1)

φ_K + φ_β = 2πn, где n = 0, 1, 2… (7.2)

Первое условие (7.1) называют балансом амплитуд, а второе – балансом фаз (7.2). Величины K и β могут зависеть от частоты ω, поэтому условия (7.1, 7.2) удовлетворяются не для всех, а только для части частот. Из-за этого в спектр автоколебаний будут входить в основном именно эти частоты, только они "выживут".

Рассмотрим ещё раз процесс самовозбуждения (условия (7.1, 7.2) выполнены): малое увеличение напряжения на входе приведёт к увеличению напряжения на выходе, а оно в свою очередь приведёт через цепочку обратной связи к ещё большему увеличению входного напряжения и так далее. Очевидно, что должен существовать механизм ограничения амплитуды – иначе такой лавинообразный процесс приведёт к нефизическому следствию бесконечного роста амплитуды. Роль такого механизма обычно играет нелинейность усилителя: коэффициент усиления уменьшается с ростом амплитуды колебаний, а амплитуда сигнала на выходе ограничена напряжением питания. Подчеркнём, что нелинейность необходима в автоколебательной системе.

LC-автогенератор

Рис. 7.1 А и Б.

Схемы простейших

LC-генераторов.

В качестве примера рассмотрим схему простейшего LC-генератора, изображённую на рис. 7.1 (автогенераторы такого вида часто называют генераторами Томсона). На схеме рис. 7.1А колебательный контур расположен в цепи стока, а на рис. 7.1Б в цепи затвора. Такие простейшие схемы сейчас применяются редко.

Рассмотрим для определённости вторую схему (рис. 7.1Б). При включении напряжения питания через транзистор начинает течь ток. Этот ток через индуктивную связь с катушкой L вызовет появление э.д.с. взаимоиндукции в цепи контура. В контуре возникнут колебания. Если знак коэффициента M взаимоиндукции выбран правильно, то напряжение на конденсаторе С, включённом между затвором и истоком транзистора, будет усиливаться и увеличивать амплитуду колебаний. Ограничение амплитуды колебаний будет происходить за счёт нелинейной зависимости коэффициента усиления от амплитуды. При установившихся автоколебаниях потери в контуре за период будут в точности компенсироваться подкачкой энергии через цепь обратной связи.

Рассмотрим более подробно работу LC-генератора. Для тока в контуре по аналогии (2.34) запишем уравнение:

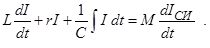(7.3)

Если формально положить правую часть этого уравнения нулю, то получим уравнение свободных колебаний в контуре. Правая часть описывает влияние усилителя. Выражая ток I_СИ через напряжение на затворе по формуле:

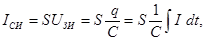где S – крутизна характеристики. Тогда:

продифференцировав и разделив на L, получим:

(7.4)

Если в (7.4) для маленького поначалу сигнала формально принять, что крутизна S является постоянной, то решение этого уравнения сразу выписывается в виде:

(7.5)

Мы видим, что член 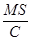, описывающий работу усилителя, эквивалентен отрицательному сопротивлению. При r > 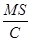в системе будут затухающие колебания, а при r < 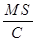– колебания с экспоненциально увеличивающейся амплитудой. Последний случай и соответствует возникновению автоколебаний.