Условия неискажённой передачи сигнала

Сигнал проходит через линейную цепь без искажений, если форма его на выходе не меняется, но могут измениться только его величина и появиться запаздывание по времени. Это возможно только в случае равномерной частотной характеристики и линейной фазовой характеристики цепи.

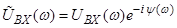Справедливость такого условия можно показать и аналитически с помощью преобразования Фурье. Пусть на вход цепи подано напряжение U_BX (t), имеющее спектральную функцию (или Фурье-образ) . Выразим это напряжение с помощью интеграла Фурье:

Пусть цепь имеет коэффициент передачи с модулем K и с фазой, линейно растущей с частотой:

(3.52)

Тогда на выходе получим напряжение, определяемое выражением

или

Окончательно U_ВЫХ (t) = K U_ВХ (t – t₀) . (3.53)

Действительно, напряжение на выходе имеет ту же форму, что и на входе, но изменено по величине в K раз и запаздывает по отношению к входному напряжению на время t₀ . Для этого в (3.52) коэффициент передачи K должен быть постоянным, а фаза, как и написано в (3.52), должна линейно расти с частотой. Это нужно для того, чтобы гармоники с большей частотой запаздывали на большее число периодов.

Обычно передача сигнала (от "входа" к "выходу") может быть описана интегро-дифференциальным оператором :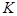

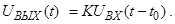
Переходя к преобразованию Фурье, можно записать это соотношение в виде:

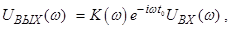
где K(ω) – комплексная рациональная функция (коэффициент передачи). Если K точно известно, то можно точновосстановить исходный сигнал, применив к полученному сигналу преобразование, обратное оператору .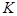

Часто удобнее (из-за технических ограничений) иметь дело не с самой функцией U_ВЫХ (t), а с рядом её дискретных отсчётов. Тогда естественно возникает вопрос, а эквивалентно ли представление функции в виде дискретных отсчётов самой функции? Здесь на помощь приходит теорема Котельникова. В зарубежной литературе она известна как теорема отсчётов – Sampling Theoremили теорема Найквиста – Nyquist-Shannon Theorem.