Понятие о дивергенции векторного поля.

Рассмотрим определение операции 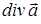в соответствии с формулой (6) предыдущего раздела. Если поток вектора 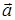через замкнутую поверхность S является, как отмечено выше, количественной мерой суммарной мощности (интенсивности) источников векторного поля 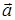в объеме V, ограниченном поверхностью S, то 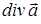представляет собой упомянутую количественную меру в пересчете на единицу объема. При этом нельзя забывать, что эта характеристика векторного поля является локальной, она получена предельным переходом V®0 в окрестности рассматриваемой точки области, занятой полем 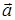. Наличие “источников” и “стоков” векторного поля проще всего продемонстрировать с помощью графических изображений векторных линий напряженности электростатического поля системы точечных положительных или отрицательных зарядов, знакомых по элементарному курсу физики. Важно отметить, что на рассматриваемых рисунках разность числа силовых линий (имеются в виду проводимые силовые линии), выходящих через произвольную замкнутую поверхность, например, сферу, и входящих в неё, изменяется только в том случае, если изменяется суммарная алгебраическая величина электрического заряда в рассматриваемой замкнутой поверхности. Если суммарный электрический заряд внутри замкнутой поверхности равен нулю, то упомянутая разность тоже обращается в нуль: число проводимых силовых линий, входящих в объём через замкнутую поверхность, равно числу проводимых силовых линий, выходящих из объёма через ту же замкнутую поверхность. На локальном уровне описания можно сказать, что в рассматриваемом случае элемент объёма не порождает новых проводимых силовых линий. Таким отличительным свойством обладают векторные поля, для которых выполнено условие 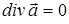во всех точках ограниченной области за исключением конечного числа “особых точек”, где расположены сосредоточенные “источники” (или “стоки”) векторного поля (в рассматриваемом случае – точечные электрические заряды).

Если рассмотреть область (для простоты – круговой цилиндр конечных размеров r < r₀ в радиальном направлении и бесконечно протяжённый в осевом направлении), в которой выполняется условие 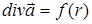> 0 , и область вне цилиндра, где выполняется условие 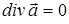, то картина проводимых векторных линий будет иметь характерный вид (рис. П.1.10):

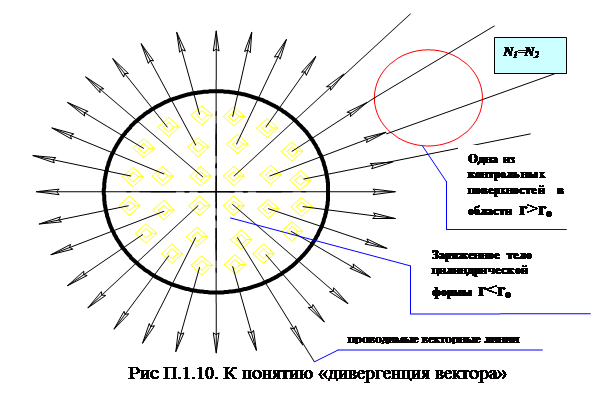
На этом рисунке легко заметить, что “новые” проводимые векторные линии появляются только в области r < r₀, т. е. там, где отлична от нуля и положительна дивергенция вектора 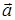. С учетом симметрии задачи число новых “проводимых векторных линии”, пересекающих произвольную замкнутую поверхность (на рисунке - произвольный цилиндр, соосный с исходным), будет расти с ростом r (в области r < r₀), а при r > r₀ их число остается постоянным. Можно, таким образом, говорить, что 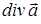пропорциональна (а при соответствующем выборе единицы измерения и равна) числу новых проводимых векторных линий в единице объема, более строго - числу новых проводимых векторных линий в элементе объёма dV, отнесенному к величине этого объёма.

Следует обратить внимание, что термин “дивергенция” переводится как “расходимость, расхождение”, однако, главным в геометрической интерпретации характера проводимых силовых линий векторного поля является не то, как они расположены, а появление “новых” или исчезновение “старых” проводимых векторных линий.

Итак, дивергенция вектора 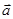представляет собой локальную количественную меру суммарной мощности (интенсивности) источников векторного поля 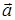в пересчете на единицу объема.