Основные теоремы теории поля.
Пусть S – замкнутая поверхность, ограничивающая объем V, М –произвольная точка объема V или поверхности S, 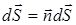 – вектор элементарной площадки на S, построенной с использованием внешней нормали
– вектор элементарной площадки на S, построенной с использованием внешней нормали 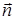 по отношению к объему V. Пусть поверхность S обладает необходимой степенью гладкости (вектор
по отношению к объему V. Пусть поверхность S обладает необходимой степенью гладкости (вектор 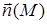 , МÎS изменяет свое направление непрерывным образом). Пусть j=j(М) – скалярная, а
, МÎS изменяет свое направление непрерывным образом). Пусть j=j(М) – скалярная, а 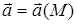 - векторная функции точки M(x,y,z). Допустим, что и j и
- векторная функции точки M(x,y,z). Допустим, что и j и 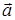 непрерывны вместе со своими первыми производными по x, y и z в любой точке объема V и его границы S. В этом случае справедливы три основные теоремы, в основе которых лежит теорема Остроградского-Гаусса, позволяющие заменить интеграл по объему на интеграл по поверхности. Три основные теоремы приводят к формулам:
непрерывны вместе со своими первыми производными по x, y и z в любой точке объема V и его границы S. В этом случае справедливы три основные теоремы, в основе которых лежит теорема Остроградского-Гаусса, позволяющие заменить интеграл по объему на интеграл по поверхности. Три основные теоремы приводят к формулам:
1. для градиента
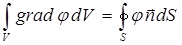 ; (1)
; (1)
2. для дивергенции
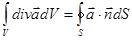 ; (2)
; (2)
3. для ротора
 . (3)
. (3)
Кроме отмеченных теорем в теории поля широко используется теорема о циркуляции (формула Стокса). Суть ее в следующем.
Если 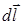 - элемент замкнутой пространственной или плоской кривой С, то справедлива формула Стокса:
- элемент замкнутой пространственной или плоской кривой С, то справедлива формула Стокса:
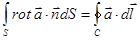 (4)
(4)
В этой формуле нормаль 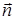 к двусторонней поверхности S, натянутой на контур С, выбирается таким образом, что положительное направление обхода контура С, если смотреть с конца вектора
к двусторонней поверхности S, натянутой на контур С, выбирается таким образом, что положительное направление обхода контура С, если смотреть с конца вектора 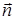 , является обходом против часовой стрелки. Иногда в математических руководствах говорят, что при обходе контура С область S остается слева. Формула Стокса позволяет заменить вычисление потока ротора векторного поля
, является обходом против часовой стрелки. Иногда в математических руководствах говорят, что при обходе контура С область S остается слева. Формула Стокса позволяет заменить вычисление потока ротора векторного поля 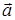 через поверхность S на вычисление циркуляции вектора
через поверхность S на вычисление циркуляции вектора 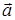 по контуру C, на который опирается поверхность S.
по контуру C, на который опирается поверхность S.
Формулы (1) – (4) позволяют дать новые определения основных дифференциальных операций векторного анализа:
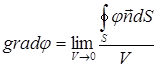 (5)
(5)
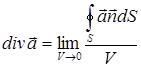 (6)
(6)
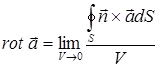 (7)
(7)
Часто для практических вычислений вместо формулы (7) используют соотношение, получаемое предельным переходом из формулы (4):
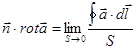 (8)
(8)
Замечательным свойством соотношений (5) – (8) является не только их символьная форма, не привязанная к конкретной системе координат, но и возможность при необходимости вычисления физических компонент соответствующих векторов в криволинейных системах координат.
Для цели настоящего курса значимость соотношений (5) – (8) заключается еще и в том, что с их помощью устанавливается физический смысл основных дифференциальных операций векторного анализа.
В теоретических построениях важную роль играет математическое утверждение о том, что из условия равенства нулю объёмного, поверхностного или линейного интеграла при любой (произвольной) области интегрирования следует локальное, справедливое в каждой произвольной точке области условие обращения в нуль подынтегральной функции.
| <== предыдущая лекция | | | следующая лекция ==> |
| Интегральные операции векторного анализа. | | | Понятие о дивергенции векторного поля. |
Дата добавления: 2017-09-01; просмотров: 1619;











