Что такое скаляр и вектор

Физические величины различной природы могут иметь различную математическую структуру описания.

Из элементарного курса известны простейшие определения скаляра (скалярной величины) и вектора (векторной величины):

¾ скаляром называется величина, которая при определенном выборе единицы измерения однозначно характеризуется числом, ее измеряющим;

¾ вектор определяется своей величиной (модулем) и направлением в пространстве и складывается с другим вектором той же физической размерности по правилу треугольника или параллелограмма.

Для описания вектора в трехмерном пространстве (рис. П.1.1) необходимо одновременно задать три параметра (три проекции, или модуль вектора и углы между направлением вектора и какими-либо двумя из трех координатных направлений). Очевидное различие в математических структурах скалярной и векторной величин приводит к различию в свойствах указанных объектов.

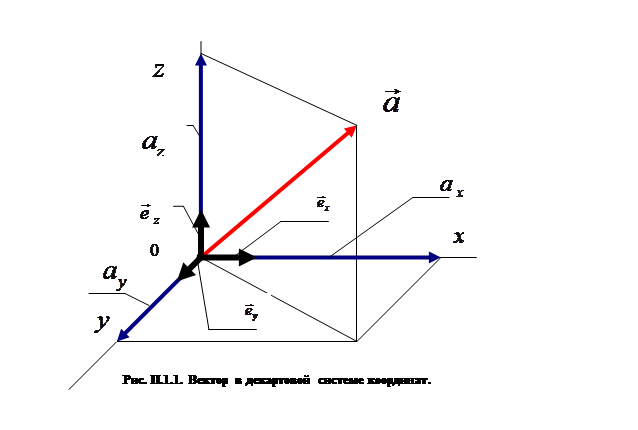
Строгая классификация физических объектов основана на изучении характера изменения их компонент при преобразованиях систем координат (т.е. при переходе от одной координатной системы к другой). В физике чаще всего имеют дело с преобразованиями систем координат в обычном трехмерном пространстве или в четырехмерном пространстве-времени Минковского.

Трансформационные свойства физических величин могут быть различны в этих случаях. К примеру, кинетическая энергия материальной точки — скаляр относительно преобразований системы координат в трехмерном пространстве и одна из компонент 4-вектора относительно преобразований в пространстве Минковского.

Важно отметить, что и вид преобразований системы координат может оказаться существенным. Так “вращения” и “сдвиги” координатных систем отличаются тем, что переводят “правые” координатные системы в “правые”, а «отражение» относительно одной из координатных поверхностей переводит «правую» координатную систему в «левую». Физическая величина может оказаться инвариантной (неизменной) при преобразовании «вращения» и неинвариантной при преобразовании «отражения».

При изучении преобразований систем координат в основной части курса мы ограничимся преобразованиями сдвига и вращения правых декартовых систем координат.

В общем, указание трансформационных свойств физической величины (т.е. ее тензорного характера) имеет смысл только по отношению к определенной группе преобразований координат в данном пространстве. С рассматриваемой точки зрения, скаляр — это величина, инвариантная относительно (разрешенных) преобразований координат, а вектор — совокупность компонент, которые при преобразовании координат трансформируются по определённому правилу, с этим правилом мы познакомимся ниже. Многокомпонентные физические объекты более сложной математической структуры, чем вектор, будут подробно описаны ниже по мере рассмотрения соответствующих физических ситуаций.

Ниже для описания скалярной величины или функции используются общепринятые обозначения. Векторные величины принято описывать или в символической форме (т.е. без указания конкретной системы координат), например, вектор 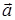, или в координатной форме 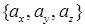, где упорядоченные величины в фигурных скобках представляют собой проекции вектора 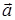на соответствующие координатные линии декартовой системы координат.

Сложение векторных величин по правилу треугольника или параллелограмма (рис. П.1.2)

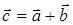
эквивалентно покоординатному сложению:

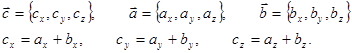
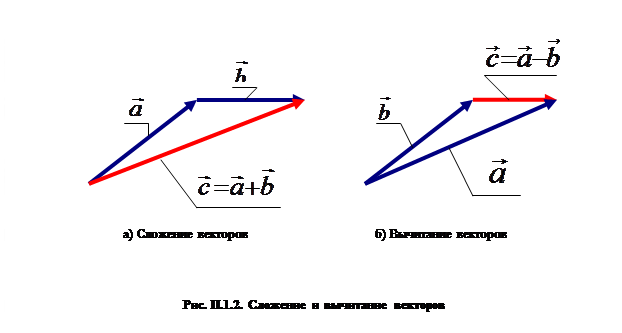
Для векторных величин определено умножение на скалярную величину:

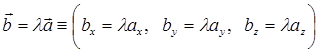
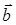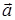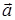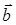Геометрический образ описанной операции очень нагляден: вектор направлен так же как и вектор , но его величина в «l раз больше» (если l>0 и размерности не имеет). Если l<0, то направление векторов и противоположны. Если l физически размерная величина, сравнить непосредственно величины векторов 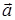и 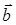не представляется возможным.

Поскольку вектор определен величиной и направлением в пространстве, его можно представить в форме:

,

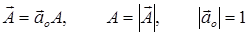где 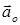– единичный безразмерный вектор (орт), совпадающий по направлению с исходным вектором 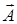; обозначение 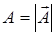используется для записи абсолютной величины (модуля) вектора .

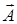Заметим, что в декартовой системе координат имеет место соотношение:

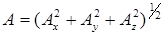
Для декартовой системы координат в трехмерном пространстве удобно ввести орты координатных линий: 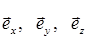(используемые иногда обозначения 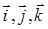не всегда удобны). В этом случае вектор 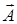можно представить в форме:

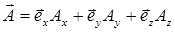
Определение операций «сложение» и «умножение на скалярную величину» позволяет ввести операцию «вычитания» векторов (рис. П.1.2) по следующему правилу:

.

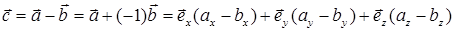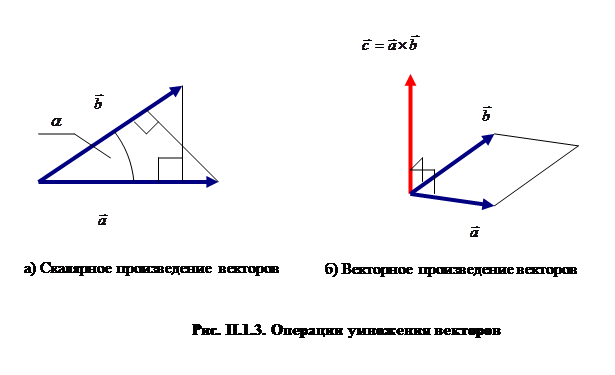
Для векторных величин известны три различные операции умножения. Первая из них, скалярное произведение двух векторов, определена правилом:

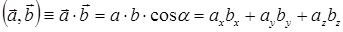
где a- угол между направлениями векторов 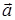и 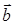, результат операции —скалярная величина (рис. П.1.3).

Если для произвольных векторов 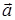и 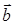, таких, что 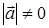и 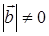, имеет место соотношение 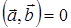, то такие векторы называются ортогональными друг другу. Геометрический смысл скалярного произведения двух векторов становится очевидным, если заметить, что выражение 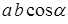представляет собой либо произведение проекции вектора 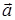на направление 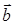на модуль вектора 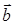, то есть 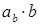, либо произведение проекции вектора 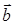на направление вектора 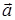на модуль вектора 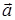, то есть 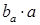. Легко проверить, что .

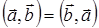Векторное произведение векторов 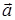и 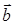определено правилом:

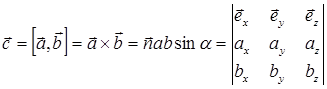
где 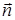– орт, направленный по нормали к плоскости, в которой расположены векторы 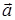и 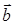, причем система направлений 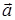, , 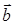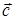является «правой» системой: кратчайшее угловое расстояние между направлениями векторов 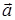и 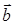(угол a) соответствует движению от 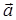к 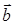против часовой стрелки, если смотреть с конца орта 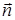(или с конца вектора 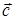). Очевидно, что направление орта нормали 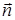совпадает с направлением вектора .

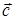Легко видеть, что результатом векторного произведения двух векторов является вектор, причем 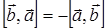. В координатной форме записи имеют место соотношения

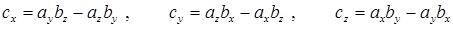
Если 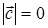, то векторы 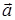и 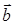либо параллельны друг другу, т.е. 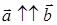, либо антипараллельны, т.е. .

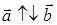Геометрический смысл векторного произведения становится наглядным, если векторы 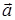и 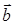представляют собой направленные отрезки двух прямых, исходящих из одной точки пространства, в этом случае величина представляет собой площадь параллелограмма, построенного на векторах 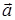и .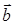

В качестве упражнения рекомендуется проверить соотношения:

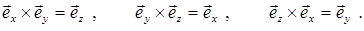
Прямое или тензорное произведение двух векторов определено следующим образом. Если имеем вектор 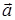, или в координатной форме 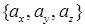, и вектор 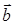, или в координатной форме {b_x,, b_y, b_z}, то можно построить двухиндексный объект – матрицу

=

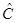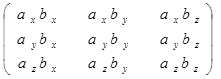
как результат тензорного произведения 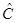= 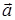Ä 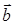, что в координатной форме имеет вид

С_ij = a_i b_j , i,j=1,2,3.

Объект, построенный таким образом, обладает свойствами тензора второго ранга. Тензоры второго и более высокого ранга используются при описании физических явлений в механике сплошных сред, электродинамике, теории относительности и т.д.

Описание алгебраических операций над векторными величинами заключим напоминанием, что операция деления векторных величин не определена.