Источники векторного поля.
Рассмотрим для простоты стационарное векторное поле 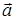 . Пусть во всем бесконечном пространстве заданы расхождение вектора
. Пусть во всем бесконечном пространстве заданы расхождение вектора 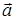 и его вихрь
и его вихрь 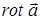 :
:
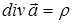 ,
, 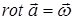 . (1)
. (1)
Скалярную величину r и векторную величину 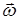 назовем «источниками» векторного поля
назовем «источниками» векторного поля 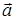 , вкладывая в эти определения тот смысл, что по заданным r=r(x,y,z) и
, вкладывая в эти определения тот смысл, что по заданным r=r(x,y,z) и 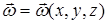 исходное векторное поле
исходное векторное поле 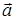 можно восстановить и эта операция однозначна при соблюдении некоторых физически объяснимых допущений о характере роста функций r и
можно восстановить и эта операция однозначна при соблюдении некоторых физически объяснимых допущений о характере роста функций r и 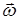 .
.
Решение задачи восстановления векторного поля по заданным его расхождению (скалярное поле) и его вихрю (векторное поле) определяется соотношением:
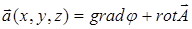 , (2)
, (2)
где
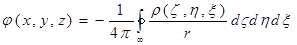 , (3)
, (3)
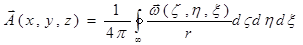 , (4)
, (4)
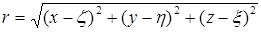 , (5)
, (5)
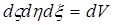 – элемент объёма. Соотношение (2) – (5) справедливы, если r(x,y,z) и
– элемент объёма. Соотношение (2) – (5) справедливы, если r(x,y,z) и 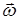 (x,y,z) непрерывны и ограниченны вместе со своими первыми производными во всем пространстве за исключением конечного числа поверхностей, где
(x,y,z) непрерывны и ограниченны вместе со своими первыми производными во всем пространстве за исключением конечного числа поверхностей, где 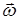 может терпеть разрыв касательной компоненты, а нормальная компонента должна оставаться непрерывной. Кроме того, должно выполняться условие
может терпеть разрыв касательной компоненты, а нормальная компонента должна оставаться непрерывной. Кроме того, должно выполняться условие 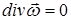 (иначе выражение (1) теряет смысл). Для существования интегралов (3) и (4) необходимо предположить, что
(иначе выражение (1) теряет смысл). Для существования интегралов (3) и (4) необходимо предположить, что
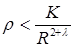 ;
;

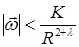 ,
, 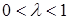 ,
,
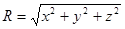 при
при 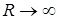 .
.
Вопрос о восстановлении поля 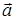 по
по 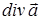 и
и 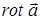 в ограниченной области пространства требует введения дополнительных так называемых граничных условий и обсуждается в специальной литературе.
в ограниченной области пространства требует введения дополнительных так называемых граничных условий и обсуждается в специальной литературе.
Принципиальная разрешимость обсуждаемой задачи имеет важное значение для выяснения свойств основных уравнений электродинамики.
| <== предыдущая лекция | | | следующая лекция ==> |
| Восстановление скалярного поля j по заданному градиенту этого поля | | | Что такое скаляр и вектор |
Дата добавления: 2017-09-01; просмотров: 1759;











