Правило преобразования компонент векторов
В основе определения вектора лежит правило преобразования компонент векторов. Аналитическая форма записи этого правила наиболее проста и компактна при использовании тензорных (координатно-индексных) обозначений. Обозначим декартовы координаты точки трехмерного пространства (x,y,z) через 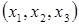 , орты координатных направлений
, орты координатных направлений 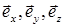 через
через 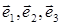 , а проекции произвольного вектора
, а проекции произвольного вектора 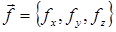 на соответствующие оси координат через
на соответствующие оси координат через 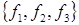 . Тройка векторов
. Тройка векторов 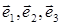 образует базис трехмерного пространства, поэтому вектор
образует базис трехмерного пространства, поэтому вектор 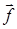 можно представить в виде:
можно представить в виде:
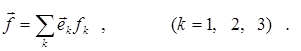 (1)
(1)
В силу взаимной ортогональности ортов 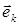 , k=1,2,3 имеем:
, k=1,2,3 имеем:
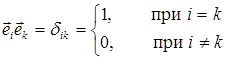 , (2)
, (2)
где 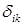 - символ Кронекера.
- символ Кронекера.
Рассмотрим две декартовы системы координат: К с базисом 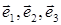 и К′ с базисом
и К′ с базисом 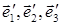 . В обеих системах используется одна и та же единица измерения. Произвольный вектор
. В обеих системах используется одна и та же единица измерения. Произвольный вектор 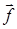 будет иметь различные представления в каждой из рассматриваемых систем,
будет иметь различные представления в каждой из рассматриваемых систем, 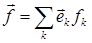 в системе К и
в системе К и 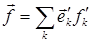
 в системе К′ (рис. П.1.4).
в системе К′ (рис. П.1.4). 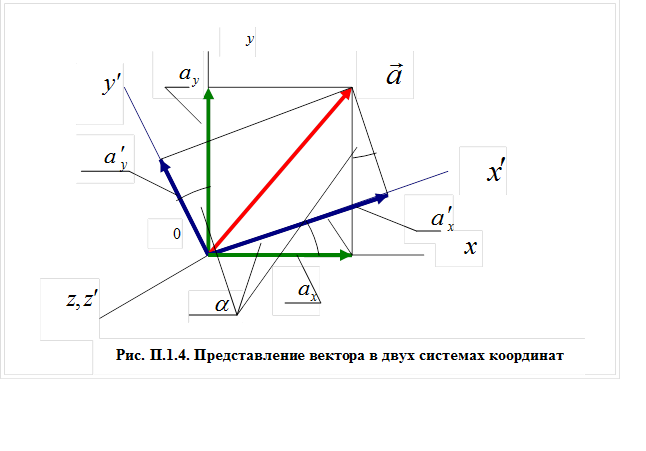 Очевидно, что должно выполняться следующее соотношение
Очевидно, что должно выполняться следующее соотношение
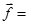
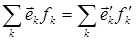
Умножим правую и левую части этого соотношения на орт 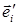 :
:
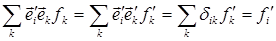 .
.
(Соотношение 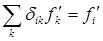 полезно проверить самостоятельно).
полезно проверить самостоятельно).
Заметим, что скалярное произведение 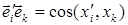 , где символом
, где символом 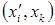 обозначен угол между направлениями соответствующих осей.
обозначен угол между направлениями соответствующих осей.
Введем обозначение 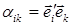 , тогда можно записать:
, тогда можно записать:
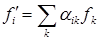 (3)
(3)
Легко видеть, что правая часть соотношения (3) представляет собой умножение матрицы 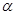 ik на вектор-столбец fi, т.е. операцию, известную из курса линейной алгебры.
ik на вектор-столбец fi, т.е. операцию, известную из курса линейной алгебры.
Из полученного соотношения следует, что компоненты вектора 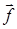 в системе координат К′ линейно связаны с его компонентами в системе координат К. Заметим, что представления вектора
в системе координат К′ линейно связаны с его компонентами в системе координат К. Заметим, что представления вектора 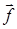 в той или иной системе координат равноправны. Именно это обстоятельство позволяет оперировать с векторными величинами безотносительно к конкретной координатной системе, т.е. в символической форме записи.
в той или иной системе координат равноправны. Именно это обстоятельство позволяет оперировать с векторными величинами безотносительно к конкретной координатной системе, т.е. в символической форме записи.
Повторяя рассуждения, благодаря которым получено соотношение (3), применительно к известному представлению вектора 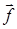 в системе координат
в системе координат 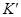 , можно получить соотношение для обратного преобразования компонент вектора (т.е. из системы К′ в систему К):
, можно получить соотношение для обратного преобразования компонент вектора (т.е. из системы К′ в систему К):
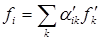 , (4)
, (4)
где 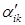 - элементы матрицы обратного преобразования
- элементы матрицы обратного преобразования 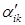 =cos(
=cos( 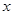 i,
i, 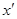 k ).
k ).
Очевидно, что двойной последовательный переход из системы К в систему К′ и снова в систему К должен привести к тождественному результату.
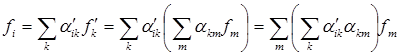
Отсюда следует, что

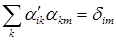 , (5)
, (5)
только в этом случае получается тождество 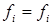 . В левой части соотношения (5) легко узнать операцию умножения матриц, а соотношение (5) в целом позволяет заключить, что матрицы (
. В левой части соотношения (5) легко узнать операцию умножения матриц, а соотношение (5) в целом позволяет заключить, что матрицы ( 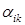 ) и (
) и ( 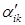 ) обратны друг другу.
) обратны друг другу.
Известно, что существование матрицы, обратной по отношению к матрице ( 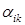 ) связано с условием
) связано с условием 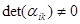 т.е. матрица преобразования (aik) не должна быть вырожденной. Преобразования, для которых матрицы перехода удовлетворяют условию
т.е. матрица преобразования (aik) не должна быть вырожденной. Преобразования, для которых матрицы перехода удовлетворяют условию 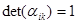 , переводят правую систему координат в правую и сохраняют неизменными метрические соотношения.
, переводят правую систему координат в правую и сохраняют неизменными метрические соотношения.
Полученные результаты можно записать в символической форме:
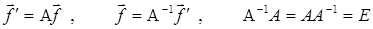 ,
,
где A - матрица прямого, A-1 - матрица обратного преобразования, а E-единичная матрица.
Не меняя формальной стороны дела, операцию перехода из системы К в систему K′ (т.е. преобразование компонент вектора 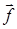 ) можно рассматривать и как трансформацию вектора
) можно рассматривать и как трансформацию вектора 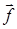 в «новую» систему координат и как операцию трансформации вектора
в «новую» систему координат и как операцию трансформации вектора 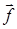 в новый вектор
в новый вектор 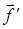 в той же самой системе координат. Первая трактовка соотношения (3) известна как “пассивная”, вторая – как “активная” (рис. П.1.4).
в той же самой системе координат. Первая трактовка соотношения (3) известна как “пассивная”, вторая – как “активная” (рис. П.1.4).
Соотношение (3) имеет настолько большое значение, что его объявляют “правилом преобразования векторов” и вектором считают только ту величину заданной структуры, для которой это правило выполняется.
Заметим, что при изучении многоэлементных величин более сложной структуры в тензорном исчислении соотношение (3) также играет определяющую роль.
Выше упоминалось, что декартовы системы координат обладают определенными преимуществами по сравнению с любыми другими системами координат при проведении общетеоретических исследований. В подтверждение этого обратим внимание читателя на то, что для декартовых координат элементы матрицы преобразования векторов 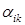 (и, соответственно,
(и, соответственно, 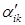 ) не зависят от рассматриваемой точки пространства (т.е. постоянны), для криволинейных координат систем их пришлось бы вычислять заново для каждой новой рассматриваемой точки пространства.
) не зависят от рассматриваемой точки пространства (т.е. постоянны), для криволинейных координат систем их пришлось бы вычислять заново для каждой новой рассматриваемой точки пространства.
В общем случае оказывается, что три компоненты одноиндексного объекта могут преобразовываться при преобразовании системы координат либо подобно преобразованию радиуса-вектора, либо подобно преобразованию дифференциальных множителей в формуле полного дифференциала скалярной величины. Общая форма линейного соотношения (3) при этом остается одинаковой, а компоненты матрицы перехода рассчитываются по разному. Компоненты первого типа называют контравариантнымикомпонентами вектора, а компоненты второго типа – ковариантными компонентами вектора. В декартовых системах координат они не различаются, а в косоугольных и криволинейных системах координат могут различаться даже своей размерностью. В практических приложениях часто говорят о проекциях вектора на координатные линии ортогональных криволинейных координат, имея в виду так называемые физические составляющие вектора. Последние представляют собой проекции вектора на направления локально введенной декартовой системы координат, оси которой являются касательными к координатным линиям криволинейной системы координат в рассматриваемой точке пространства. Физические составляющие вектора в криволинейной системе координат не подчиняются правилу (3) и по этой причине не составляют вектор в полном смысле этого определения.
| <== предыдущая лекция | | | следующая лекция ==> |
| Что такое скаляр и вектор | | | Дифференциальные операции векторного анализа |
Дата добавления: 2017-09-01; просмотров: 2163;











