Теорема Гаусса в интегральной форме.

"Поток вектора напряжённости электростатического поля через произвольную неподвижную замкнутую поверхность равен суммарному электрическому заряду, находящемуся внутри этой поверхности (с точностью до сомножителя, определяемого выбором системы единиц измерения)".

В системе СИ:

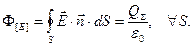
Эта теорема - одна из важнейших теорем электромагнетизма. Докажем её для общего случая на физическом уровне строгости. Доказательство проводится в четыре этапа.

Первый этап.

Рассмотрим точечный (сосредоточенный) электрический заряд, расположенный в начале координат. Векторное поле напряжённости при этом, как мы видели в лекции 1, имеет вид:

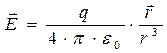
здесь 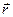- радиус-вектор точки наблюдения, 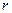- расстояние точки наблюдения от начала координат. Пусть замкнутая поверхность является сферой с центром в начале координат и с радиусом :

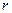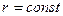
Единичная нормаль к этой поверхности определяется выражением:

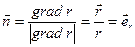
(см. предыдущую лекцию). Запишем:

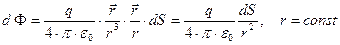
Интегрируем по поверхности сферы:

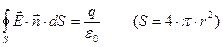
Для частного случая теорема Гаусса доказана (прямым вычислением).

Второй этап. Усложним проблему: пусть замкнутая поверхность не является сферой, пусть она достаточно гладкая, а в остальном практически произвольная. В этом случае:

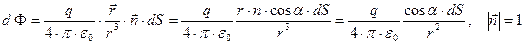
Заметим:

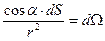
где 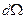- элементарный телесный угол, под которым из начала координат видна площадка dS. Из геометрии известно, что любая замкнутая поверхность из начала координат видна под телесным углом 4 "пи" стерадиан, если она содержит начало координат внутри себя, и суммарный телесный угол "видности замкнутой поверхности" равен нулю, если начало координат не лежит внутри этой поверхности. 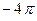Последнее относится и к случаю, ели рассматривается область между двумя концентрическими сферами: угол внешней сферы , а внешней , в сумме - это нуль.

Замечание. Надо иметь в виду, в теореме Гаусса рассматривается внешняя по отношению к объёму единичная нормаль. Это важно. В приложениях можно придти к неверным результатам из-за потери знака.

Что в итоге? В итоге мы получаем, что для рассматриваемого случая

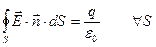
справедливо.

Третий этап.

Точечный заряд находится в произвольной точке пространства. Замкнутая поверхность - произвольная. Перенесём начало координат в точку пространства, где расположен электрический заряд. При этом, естественно, поменяется уравнение рассматриваемой замкнутой поверхности, но остаётся в силе результат предыдущего этапа. Значит, и в этом случае теорема Гаусса справедлива.

Четвёртый этап.

Если доказательство проходит для точечного (сосредоточенного) электрического заряда, то (вспомним методу использования принципа суперпозиции для вектора напряжённости электростатического поля) можно считать доказанной теорему Гаусса для произвольного распределения электрического заряда в пространстве.