Теорема Гаусса для электростатического поля.
Содержание.
Поток вектора напряжённости электрического поля. Теорема Гаусса в интегральной и дифференциальной формах в вакууме и её применение для расчёта электростатических полей. Уравнение Пуассона.
Следствием закона Кулона является определение понятия "напряжённость электростатического поля". Позже будет доказано, что векторное поле 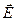
существует как объективная физическая реальность, хотя в рамках электростатики (неподвижные заряды) с равным успехом можно пользоваться теорией взаимодействия электрических заирядов и теорией действия электростатического поля на электричесукий заряд. Напряжённость электростатического поля (как векторное поле) обладает рядом физических (и математических) свойств. Для этого поля применим принцип суперпозиции. Это поле является потенциальным.
В этой лекции познакомимся с ещё одним замечательным свойством напряжённости электростатического поляв
Поток векторного поля (в просторечии - поток вектора).
Рассмотрим векторное поле 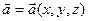 в окрестности точки М :
в окрестности точки М : 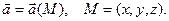
Пусть в окрестности рассматриваемой точки расположен малый элемент поверхности, площадь которого равна dS, и выбран один (из двух возможных) вариант единичной нормали
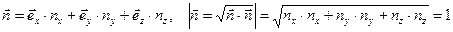
к элементу поверхности dS . Определим малый элемент поверхности как векторную величину:
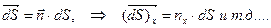
Образуем скалярное произведение:
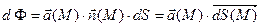 (*)
(*)
Определение: 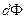 - элементарный поток векторного поля
- элементарный поток векторного поля 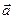 через площадку
через площадку 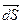 , площадь которой равна модулю вектора
, площадь которой равна модулю вектора 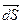 , направление нормали определено вектором
, направление нормали определено вектором 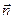 , все рассматриваемые величины определены в точке пространства М.
, все рассматриваемые величины определены в точке пространства М.
Величина 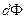 - скалярная (алгебраическая) величина.
- скалярная (алгебраическая) величина.
Проинтегрируем выражение (*) по произвольной поверхности:
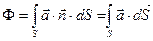
Если поверхность интегрирования "замкнутая", употребляется специальный символ интеграла:
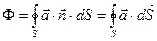
Приведённые выше выражения - поток векторного поля 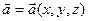 через поверхности S.
через поверхности S.
Выражение "поток вектора" пришло в математику из механики сплошной среды. Если 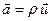 - плотность потока массы, то
- плотность потока массы, то 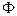 - количество протекающей через поверхность S массы за единицу времени, т.е. "расход массы".
- количество протекающей через поверхность S массы за единицу времени, т.е. "расход массы".
Дата добавления: 2017-09-01; просмотров: 993;










