Практическое использование теоремы Гаусса для напряжённости электростатического поля в вакууме.

Дифференциальная форма теоремы.

Декартовые координаты:

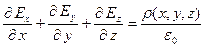
Цилиндрические координаты:

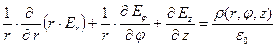
Сферические координаты:

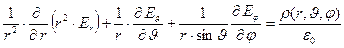
Во всех случаях имеем три неизвестных функции (проекции вектора 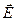на соответствующие координатные направления) и одно скалярное уравнение. Решить это уравнение можно либо для одномерного случая (поле 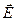имеет одну отличную от нуля компоненту), либо для случая, когда каким-либо образом установлены дополнительные зависимости между неизвестными компонентами. Распределение объёмной плотности электрического заряда должно быть согласовано с условиями, накладываемыми на компоненты вектора напряжённости электростатического поля.

Примеры.

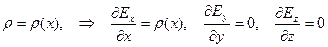
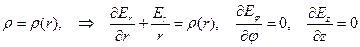
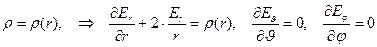
Можно заметить, что в приведённых примерах прослеживается определённая симметрия задачи.

Интегральная форма теоремы.

Рассмотрим случай сферически симметричного распределения объёмной плотности электрического заряда

Рассмотрим случай распределения объёмной плотности электрического заряда в условиях осевой симметрии.