В аналитической форме.
Рассмотрим пример с кривошипно-ползунным механизмом.
К основным размерам, характеризующим кинематическую схему механизма относятся:
1. длина кривошипа - 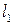
2. относительная длина шатуна - 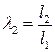
3. относительная внеосность - 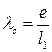
4. угол наклона направляющей ползуна - 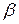
5. начальная угловая координата звена 1 - 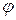
Изобразим кинематическую схему механизма:
|
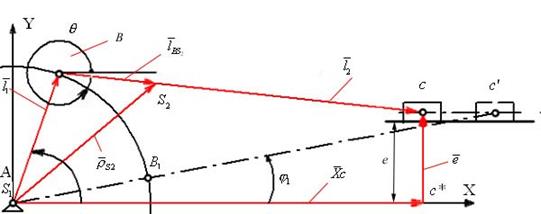
Условие замкнутости векторного контура 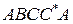 для любого положения механизма выражается уравнением:
для любого положения механизма выражается уравнением:
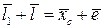
Проецируя этот векторный контур на оси координат 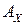 и
и 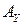 получим функцию положения механизма, т.е. зависимость входной координаты
получим функцию положения механизма, т.е. зависимость входной координаты 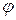 и входной координаты
и входной координаты 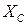 :
:
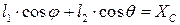 (5.1)
(5.1)
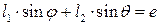 (5.2)
(5.2)
Из уравнения (5.2) угловая координата 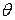 вектора
вектора 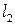 определяется по формуле:
определяется по формуле:
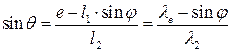 (5.3)
(5.3)
где 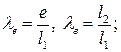
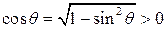 (5.4)
(5.4)
Дифференцируя (5.1) по обобщённой координате 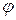 получим:
получим:
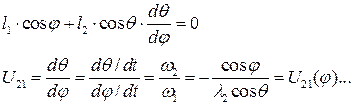 (5.5)
(5.5)
Дифференцируя (5.2) по 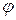 получим:
получим:
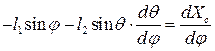
Передаточная функция скорости точки С:
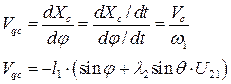 (5.6)
(5.6)
Из векторного контура 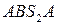 определим радиус-вектор центра масс:
определим радиус-вектор центра масс:
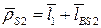
Проецируя этот векторный контур на оси координат 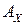 и
и 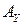 , получим координаты центра масс
, получим координаты центра масс 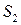 :
:
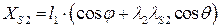 (5.7)
(5.7)
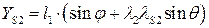 (5.8)
(5.8)
Дифференцируя (5.7) и (5.8) по 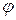 получим проекции передаточной функции скорости точки
получим проекции передаточной функции скорости точки 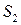 :
:
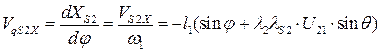 (5.9)
(5.9)
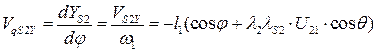 (5.10)
(5.10)
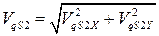
Дифференцируя по 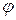 выражение (5.5) получим проекции передаточной функции ускорения звена 2 (шатуна):
выражение (5.5) получим проекции передаточной функции ускорения звена 2 (шатуна):
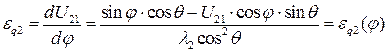 (5.11)
(5.11)
Дифференцируя по 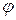 выражение (5.6) получим передаточную функцию ускорения точки С:
выражение (5.6) получим передаточную функцию ускорения точки С:
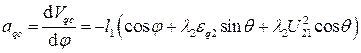 (5.12)
(5.12)
Аналогично можно получить кинематические передаточные функции ускорения точки 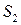 , если продиффиринцировать (5.9) и (5.10) по
, если продиффиринцировать (5.9) и (5.10) по 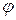 :
:
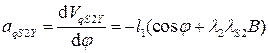 (5.13)
(5.13)
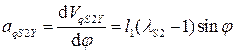 (5.14)
(5.14)
где 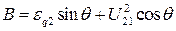 (5.15)
(5.15)
Для общего случая движения механизма, когда 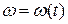 :
:
Угловое ускорения шатуна:
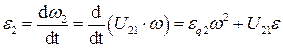 (5.16)
(5.16)
Ускорение ползуна:
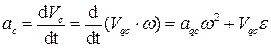 (5.17)
(5.17)
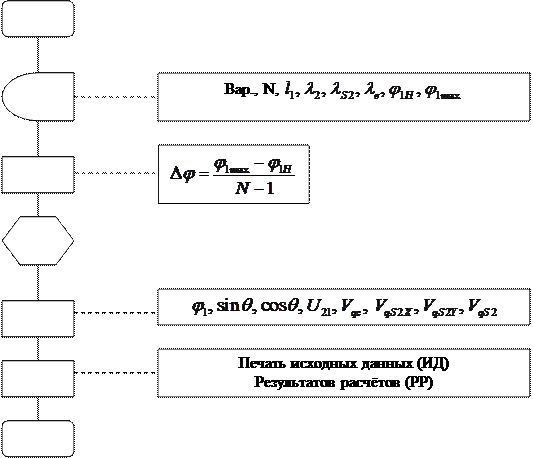
Блок-схема программы определения кинематических передаточных функций скорости кривошипно-ползунного механизма (AR210):
Метод планов положений, скоростей и ускорений
Кинематические характеристики кривошипно-ползунного (и любого другого) механизма могут быть определены и с помощью графоаналитического метода или как его чаще называют метода планов наложений скоростей и ускорений.
Планом механизма называется масштабное графическое изображение кинематической схемы механизма соответствующее заданному положению входного звена.
Планом скоростей механизма называется чертёж, на котором изображены в виде отрезков векторы, равные по модулю и направлению скоростям различных точек механизма в данный момент.
Чертёж, на котором изображены в виде отрезков векторы, равные по модулю и направлению ускорениям различных точек звеньев механизма в данный момент, называют планом ускорений механизма.
Для иллюстрации этого метода постоим план скоростей (рис. 5.4) для той же угловой координаты 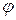 . Если угловая скорость
. Если угловая скорость 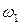 задана, то строим план скоростей в масштабе
задана, то строим план скоростей в масштабе 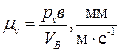 , Если же
, Если же 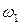 неизвестна, то строим план возможныхскоростей.
неизвестна, то строим план возможныхскоростей.
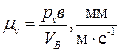
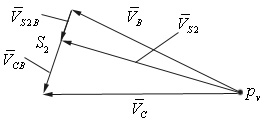 Определение скоростей.
Определение скоростей.
Векторные уравнения для определения скоростей точек В, С и S2:
|
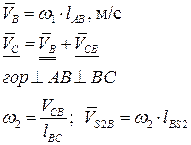
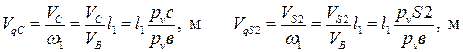
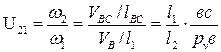
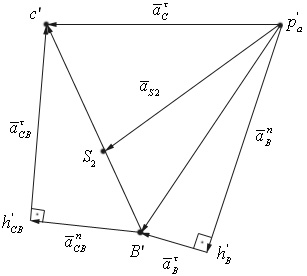 Определение ускорений
Определение ускорений
Для определения ускорений точек В и С записываем уравнения в следующем виде:
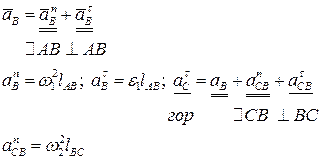
|
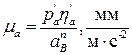 . Угловое ускорение шатуна (звена 2) определяем по формуле:
. Угловое ускорение шатуна (звена 2) определяем по формуле:
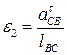 .
.
Дата добавления: 2017-02-13; просмотров: 1577;











